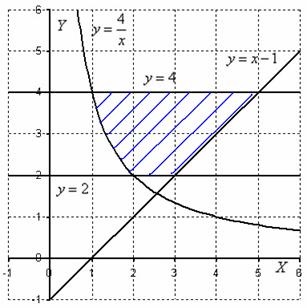
Începem să analizăm procesul propriu-zis al calculului integratului dublu și să ne cunoaștem sensul geometric.
Integralul dublu este numeric egal cu aria figurii plane (regiunea de integrare). Aceasta este cea mai simplă formă a unui integral dublu, atunci când funcția a două variabile este egală cu una :.
Mai întâi considerăm problema în formă generală. Acum esti mult surprins de cat de simplu este totul! Să calculam suprafața unei figuri plane. delimitată de linii. Pentru claritate, presupunem că în intervalul respectiv. Zona acestei cifre este numeric egală cu:
Desenați zona pe desen:
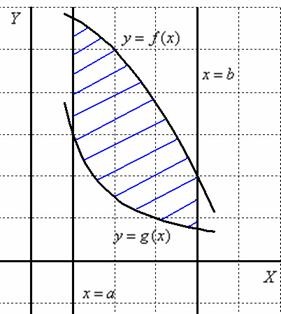
Să alegem primul mod de ocolire a zonei:
Și imediat o tehnică tehnică importantă: integrale repetate pot fi luate în considerare separat. Mai întâi, integralele interioare, apoi integralele exterioare. Această metodă este recomandată în mod serios începătorilor în subiectul ceainicilor.
1) Calculăm integrala interioară, în timp ce integrarea se face peste variabila "yerk":
Nedefinită Integrala aici este simplu, banal și apoi folosit Newton-Leibniz formulă, singura diferență este că limitele de integrare nu sunt numere, și funcții. În primul rând, limita superioară a fost stabilită în "jucătorul" (funcția primitivă), apoi limita inferioară
2) Rezultatul obținut în primul paragraf trebuie înlocuit în integralul exterior:
O înregistrare mai compactă a întregii soluții arată astfel:
Formula obtinuta este tocmai formula de lucru pentru calcularea suprafetei unei figurante plane folosind integrala definita "obisnuita"! Consultați lecția Calculând zona folosind un integrat definit. acolo este la fiecare pas!
Asta este, problema de a calcula zona cu ajutorul integrat dublu diferă puțin de problema de a găsi zona cu ajutorul unui integral integrat! De fapt, acesta este același lucru!
În consecință, nu ar trebui să apară dificultăți! Nu voi lua în considerare foarte multe exemple, deoarece, de fapt, v-ați confruntat în mod repetat cu această sarcină.
Folosind integralele duble, se calculează suprafața planului. delimitată de linii.
Soluție: Desenați zona din desen:
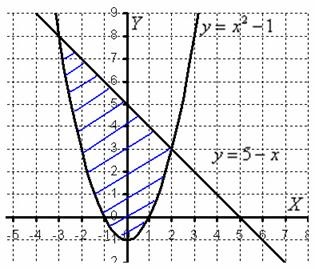
Zona figurului este calculată cu ajutorul integratului dublu prin formula:
Alegem următoarea ordine de traversare a domeniului:
Aici și în continuare nu voi mai vorbi despre cum să efectuăm o eludare a regiunii, deoarece în prima secțiune s-au dat explicații foarte detaliate.
Așa cum am menționat deja, este mai bine ca începătorii să calculeze separat integralele repetate și voi urma aceeași metodă:
1) Mai întâi folosim formula Newton-Leibniz pentru a rezolva integralele interne:
2) Rezultatul obținut în prima etapă este înlocuit în integralele exterioare:
Paragraful 2 - găsirea reală a zonei unei figuri plane cu ajutorul unui integrat definit.
Iată o sarcină atât de stupidă și naivă.
Exemplul curios pentru auto-soluție:
Folosind integralele duble, se calculează suprafața planului. delimitată de linii. .
Un exemplu de eșantion de finalizare a soluției la sfârșitul lecției.
În exemplele 9-10 este mult mai avantajos să utilizați prima cale în jurul zonei, cititorii curioși, apropo, puteți schimba ordinea bypass-ului și puteți calcula ariile în al doilea rând. Dacă nu faceți o greșeală, atunci, firește, vor fi obținute aceleași valori ale zonelor.
Dar, într-o serie de cazuri, cea de-a doua metodă de ocolire a regiunii este mai eficientă și, în încheierea cursului tânărului botanist, vom lua în considerare câteva exemple de mai sus pe această temă:
Folosind integralele duble, se calculează suprafața planului. delimitată de linii.
Soluție: suntem așteptați cu nerăbdare de două parabole cu un bzik care se află pe laturile lor. Nu trebuie să zâmbești, lucruri similare se întâmplă de multe ori în integrale.
Care este cel mai simplu mod de a face un desen?
Reprezentăm parabola sub forma a două funcții:
- ramura superioară și - ramura inferioară.
În mod similar, reprezentăm parabola sub forma ramurilor superioare și inferioare.
Apoi, graficul punct-cu-punct al grafurilor conduce, rezultând într-o astfel de cifră bizară:
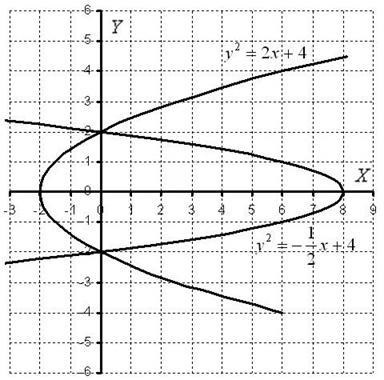
Zona figurului este calculată cu ajutorul integratului dublu prin formula:
Ce se întâmplă dacă alegem prima cale în jurul zonei? În primul rând, această zonă va trebui împărțită în două părți. Și în al doilea rând, vom observa această imagine trista :. Integralele, desigur, nu sunt super complicate, dar ... există o propoziție matematică veche: una care este prietenoasă cu rădăcini, care nu este necesară.
Prin urmare, din neînțelegerea, care este dată în condiție, exprimăm funcțiile inverse:
Funcțiile inverse din acest exemplu au avantajul că au pus imediat întreaga parabolă fără frunze, ghinde de ramuri și rădăcini.
Conform celei de-a doua metode, ocolirea regiunii va fi după cum urmează:
În acest fel:
După cum spun ei, simți diferența.
1) Îndreptați-vă cu integrarea internă:
Înlocuim rezultatul în integralul exterior:
Integrarea variabilei "joc" nu ar trebui să fie jenantă, ar fi o literă "zu" - ar fi minunat să se integreze peste ea. Deși cineva citește al doilea paragraf al lecției Cum se calculează volumul corpului de rotație. el nu se confruntă deja cu cea mai mică stânjenire cu integrarea "igrik".
Ce să adăugați .... Totul!
Pentru a testa tehnica de integrare, puteți încerca să calculați. Răspunsul ar trebui să fie exact același lucru.
Folosind integralele duble, se calculează suprafața planului. delimitată de linii
Acesta este un exemplu de auto-decizie. Este interesant de observat că, dacă încercați să utilizați prima cale în jurul zonei, atunci cifra va trebui împărțită în două părți în loc de două! Și, în consecință, se obțin trei perechi de integrale repetate. Se întâmplă și așa.
Clasa de master a ajuns până la sfârșit și este momentul să se mute la nivelul mastermasterului. - Cum să calculezi integralele duble? Exemple de soluții. Voi încerca în al doilea articol, deci nu fi lame =)
Soluții și răspunsuri:
Exemplul 2: Soluție: Desenați desenul de zonă:
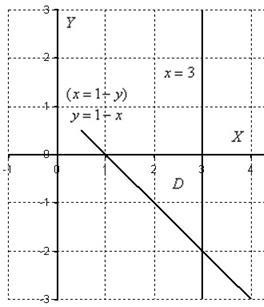
Alegem următoarea ordine de traversare a domeniului:
În acest fel:
Trecem la funcțiile inverse:
Să schimbăm ordinea bypass-ului regiunii:
În acest fel:
răspundă:
Exemplul 4: Soluție: Să trecem la funcțiile directe:
Să executăm desenul:
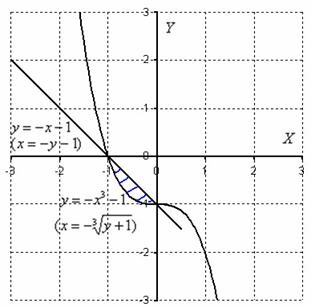
Să schimbăm ordinea bypass-ului regiunii:
răspundă:
Exemplul 6: Soluție: Să executăm desenul:
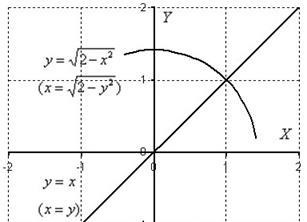
Trecem la funcțiile inverse:
Modificăm ordinea integrării prin împărțirea regiunii de integrare în două părți. În acest caz, ordinea bypass-ului regiunii:
1), 2)
răspundă:
Exemplu 8: Soluție: Desenați zona de integrare pe desen:
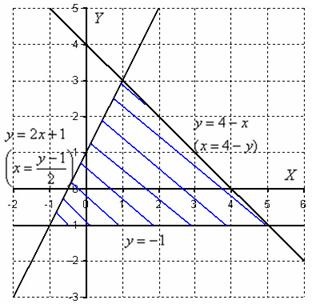
Trecem la funcțiile inverse:
Să schimbăm ordinea traversării corporale:
răspundă:
Exemplul 10: Soluție: Desenați desenul de zonă:
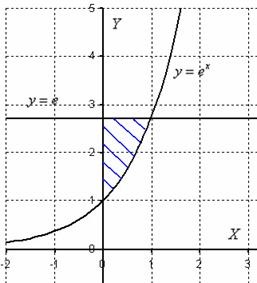
Zona figurului este calculată cu ajutorul integratului dublu prin formula:
Alegem următoarea ordine de traversare a domeniului:
În acest fel:
1)
2)
răspundă:
Exemplul 12: Soluție: Desenați această figură pe desen: