Majoritatea problemelor legate de apartenența punctelor și a avioanelor drepte pot fi rezolvate, conduse de două propoziții.
1) O linie aparține unui plan dacă două puncte ale unei linii aparțin acestui plan sau dacă au un punct comun cu un plan și sunt paralele cu o linie dreaptă situată în acest plan (Figura 23, linia l).
2) Punctul aparține planului dacă este pe o anumită linie dreaptă în acest plan (Figura 23, punctele N și K).
Să ilustrăm aceste dispoziții cu un exemplu.
Construiți o proiecție orizontală a liniei drepte l. situată în # 8710; ABC (figura 23).
Gasim doua puncte comune pentru linia l si avionul # 8710; ABC. Aceasta este proiecția punctului A2 și punctul de intersecție 12 al proiecției liniei 12 cu proeminența laturii B2 C2. Construind o proiecție orizontală a punctului 11. tragem prin el proiecția orizontală dorită a liniei drepte l (l1).
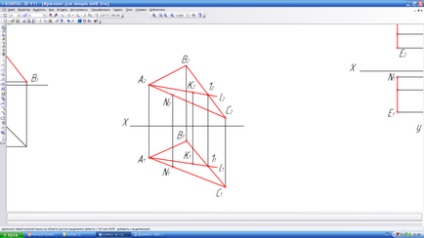
Liniile principale ale planului sau liniei planului de nivel (Figura 24)
În plan, pot fi trase un număr infinit de contururi, fronturi și linii drepte de profil (a se vedea Problema 16 din registrul de lucru al IG).
1) Partea din față (/) este linia dreaptă care aparține planului u // n2;
2) Orizontul (h) este o linie dreaptă care aparține planului și / n1;
3) Profilul (p) este o linie dreaptă care aparține planului și // N3;
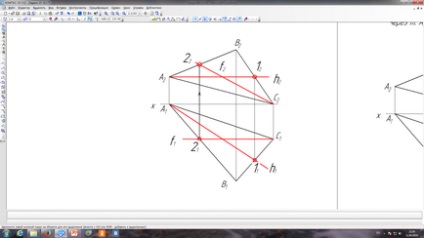
Poziția reciprocă a liniilor drepte și a planurilor
Este necesar să se identifice și să se bazeze pe diagrama linie dreaptă paralelă cu planul și o linie care se intersectează cu planul, două planuri paralele și două planuri care se intersectează, linii drepte perpendicular pe planul și perpendicular pe planul.