Caracteristicile statistice de bază ale unui proces aleator staționar
În Fig. 5.2 prezintă implementarea unui proces aleator staționar.
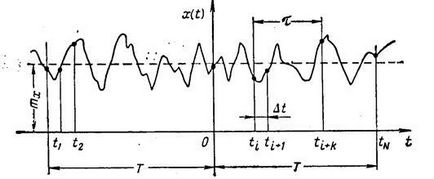
Să determinăm caracteristicile statistice de bază ale unui proces aleatoriu staționar
Valoarea medie a semnalului pe un interval de timp finit este definită ca:
Dacă intervalul este suficient de mare, atunci valoarea medie determină așteptările matematice
Dacă, în practică, implementarea finală este reprezentată ca valori discrete separate între ele prin intervale egale de timp, atunci valoarea medie poate fi calculată prin formula:
Un proces aleator staționar poate fi considerat ca fiind suma unei componente constante și a unei componente alternante corespunzătoare deviațiilor semnalului aleatoriu de la media:
Un semnal se numește un semnal aleator central. Evident, valoarea medie a unui semnal aleator centrat este zero. Deoarece spectrul semnalului real coincide cu spectrul semnalului aleator centrat, în multe (dar nu toate) probleme de calcul al sistemelor automate, se poate lua în considerare semnalul.
Dispersia este valoarea medie a pătratului abaterilor de la așteptările matematice:
- aceasta este o măsură a răspândirii valorilor instantanee ale semnalului în apropierea așteptărilor matematice. Cu cât e mai mult, cu atât mai mult
O abatere patratică medie este o expresie a formei:
O proprietate importantă a caracteristicilor statice este următoarea:
Asteptarile matematice si variatia sunt caracteristici importante, dar ele nu sunt exhaustive: ele nu pot fi folosite pentru a judeca rata de schimbare a unui semnal in timp
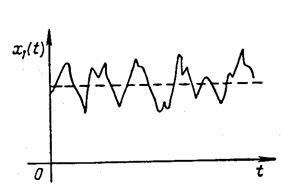
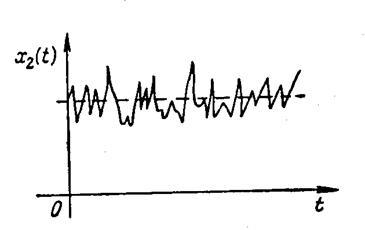
Figurile 5.3, 5.4 arată procese aleatorii staționare având așteptări și variații matematice egale (). Cu toate acestea, din cifre se poate observa că se schimbă mai lent decât. Intensitatea variației unui proces aleator staționar în timp este caracterizată de următoarele funcții: funcția de corelare și funcția de densitate spectrală.
Funcția de corelare (autocorelație) este așteptarea matematică a produsului din valorile instantanee ale semnalului separate de un interval de timp:
Pentru un semnal centrat, funcția de corelare este determinată de formula:
unde este variabila de timp:
O valoare numerică fixă corespunde unei valori fixe.
Funcția de corelare caracterizează gradul de corelare (conexiune) între valorile anterioare și cele ulterioare ale semnalului.
Funcția de corelare are următoarele proprietăți:
1. Cu o creștere a relației (corelație) se slăbește.
2. Funcția de corelare scade mai repede cu cât se schimbă mai repede semnalul aleatoriu.
3. Funcția de corelare este o funcție uniformă:
În mod experimental, funcția de corelare este determinată (calculată) în conformitate cu următoarea schemă: