Metoda lui Newton este cea mai eficientă metodă pentru rezolvarea ecuațiilor neliniare. Lasă rădăcina. t. e .. Presupunem că funcția este continuă pe interval și de două ori continuu diferențiată pe interval. Să o punem. Desenați o tangență la graficul funcției în acest punct (Figura 1.8).
Ecuația tangentei va arăta astfel :.
Prima intersecție se obține luând abscisa punctului de intersecție a acestei tangente cu axa. adică, punerea.
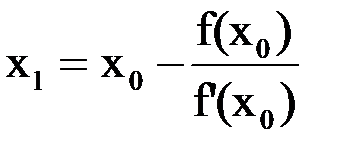
În mod similar, procedăm cu punctul. apoi cu un punct etc., ca rezultat vom obține o secvență de aproximări. și
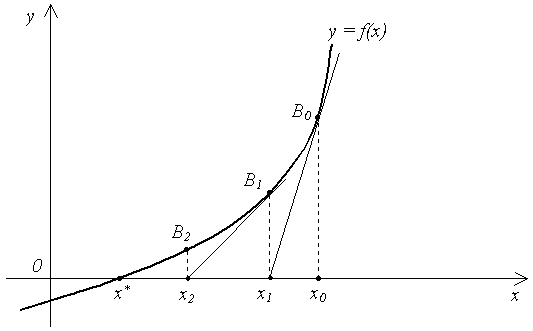
Figura 1.8 - Tangentă la graficul unei funcții la un punct
Formula (1.6) este formula de calcul pentru metoda Newton.
Metoda Newton poate fi considerată ca un caz special al metodei iterațiilor simple, pentru care
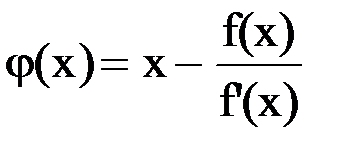
Convergența metodei. Convergența metodei lui Newton este stabilită de următoarea teoremă.
Teorema. Fie o rădăcină simplă a ecuației și în unele zone din această rădăcină funcția este de două ori continuu diferențiată. Apoi, există un mic cartier de rădăcină. că pentru o alegere arbitrară a apropierii inițiale față de această vecinătate, secvența de iterație definită de (1.6) nu depășește această vecinătate și se aplică următoarea estimare:
Convergența metodei lui Newton depinde de cât de aproape de rădăcină este aleasă aproximarea inițială.
Alegerea aproximării inițiale. Fie segmentul care conține rădăcina. Dacă, ca aproximație inițială, alegeți unul dintre capetele segmentului pentru care. atunci iterațiile (1.6) converg și monotonice. Figura 8 corespunde cazului în care capătul din dreapta al segmentului a fost ales ca aproximație inițială: (aici).
Eroarea metodei. Estimarea (1.7) este incomodă pentru utilizarea practică. În practică, se utilizează următoarele estimări de eroare:
Criteriul de terminare. Estimarea (1.8) ne permite să formulăm următorul criteriu pentru terminarea iterațiilor metodei Newton. Pentru o anumită precizie, calculul trebuie efectuat până la inegalitate
.
Exemplul 1.3. Calculați prin metoda Newton rădăcina negativă a ecuației la valoarea de 0,0001. După separarea rădăcină, putem verifica dacă rădăcina este localizată pe interval. În acest interval și. Deoarece și. atunci se poate lua aproximația inițială.
Tabelul 1.3 - Valori de proiectare