O linie dreaptă este unul dintre conceptele de bază ale geometriei.
Prezentarea sistematică linie dreaptă geometria este, de obicei, presupune unul dintre conceptele de bază, ceea ce a determinat doar indirect geometria axiome.
Dacă conceptul de distanță între două puncte ale spațiului servește drept bază pentru construirea geometriei, atunci o linie dreaptă poate fi definită ca o linie de-a lungul căreia calea este egală cu distanța dintre două puncte.
Analitic, linia este dată de o ecuație (într-un spațiu tridimensional - un sistem de ecuații) de gradul I.
Proprietățile unei linii în geometria euclidiană
- Prin intermediul a două puncte care nu coincid, se poate desena o singură linie dreaptă.
- Două linii disjuncte din plan se intersectează la un singur punct sau sunt paralele.
- În spațiul tridimensional, există trei variante ale aranjării reciproce a două linii drepte:
- drepte se intersectează;
- liniile drepte sunt paralele;
- direct traversat.
- O linie dreaptă este o linie algebrică de ordinul întâi: într-un sistem de coordonate cartezian, o linie dreaptă este dată pe plan cu o ecuație de gradul I (ecuația liniară).
Ecuațiile unei linii în plan
Metode pentru specificarea unei linii:
sau
Ecuația generală a unei linii drepte pe plan în coordonate carteziene:
unde A și B nu sunt simultan egale cu zero. Pentru C = 0, linia trece prin origine.
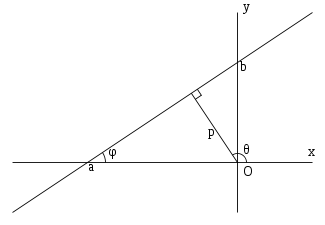
Ecuația unei linii drepte cu un coeficient unghiular. O linie dreaptă ce intersectează axa Oy într-un punct și formează un unghi φ cu o direcție pozitivă a axei Ox:
Coeficientul k este numit panta liniei drepte. În această formă, este imposibil să ne imaginăm o linie dreaptă paralelă cu axa Oy.
Ecuația unei linii în segmente. O linie dreaptă care intersectează axa Ox în punctul respectiv și axa Oy la punctul:
În această formă, este imposibil să ne imaginăm o linie dreaptă care trece prin origine.
unde p - lungimea perependikulyara a scăzut la linia de origine, și θ - unghiul (măsurat în direcția pozitivă) între direcția pozitivă a axei Ox și direcția perpendiculara. Dacă p = 0, atunci linia trece prin origine, iar unghiul determină unghiul liniei drepte.
Dacă linia este dată de ecuația generală Ax + By + C = 0. atunci segmentele a și b. tăiată de ea pe axe, coeficientul unghiular k. distanța de la originea coordonatelor p. cosθ și sinθ sunt exprimate prin coeficienții A. B și C după cum urmează:
Pentru a evita semnul incertitudinii înainte de radicalul este ales să respecte termenii p> 0. În acest caz, cosθ și sinθ sunt cosinus direcția de pozitive normale drepte - perpendicular de la origine pe linie. Dacă C = 0, atunci linia trece prin origine și alegerea direcției pozitive este arbitrară.
Ecuația unei linii drepte care trece prin două puncte necoincidențe date și
sau în formă generală
Ecuațiile parametrice ale unei linii drepte pot fi scrise sub forma:
unde t este parametrul derivat, în acest caz
Ecuația tangențială a unei linii drepte în plan:
Numerele ξ și η sunt numite tangențiali. liniare sau Plücker.
Ecuațiile unei linii în spațiu
Ecuația canonică a unei linii în spațiu:
Fie M (x0, y0, z0) un punct situat pe o linie, iar u este un vector colinar cu el. Apoi ecuația liniei drepte are forma:
Aranjamentul reciproc de puncte și linii
Trei puncte și se află pe o linie dacă și numai dacă este condiție
Abaterea punctului de la linia Ax + By + C = 0 poate fi găsită prin formula
unde semnul din fața radicalului este opus semnalului C. Abaterea în modul este egală cu distanța dintre punct și linia dreaptă; este pozitiv dacă punctul și originea coordonatelor se află pe laturile opuse ale liniei și negative dacă pe o parte.
Aranjamentul reciproc al mai multor linii drepte
Două linii drepte date de ecuații
se intersectează într-un punct
Unghiul γ12 între liniile intersectate este definit de formula
Astfel, sub γ12 înțeles unghiul cu care este necesar să se rotească prima linie dreaptă (A1 predeterminate parametri. B1. C1. K1 și b1), în jurul punctului de intersecție în sens antiorar până când primul aliniament cu a doua linie.
Aceste linii sunt paralele. dacă A1B2 este A2B1 = 0 sau k1 = k2. și perpendicular. dacă A1A2 + B1B2 = 0 sau
Dacă semnul din fața radicalului este opusul lui C1. atunci δ este pozitivă atunci când a doua linie și originea se află pe laturile opuse ale primei linii drepte.
Pentru trei linii drepte
intersectate la un punct sau paralele între ele, este necesară și suficientă această condiție
Vedeți ce înseamnă "Ecuațiile directe" în alte dicționare:
Ecuațiile de mișcare - ecuația mișcării (ecuația de mișcare), ecuația sau sistemul de ecuații care definesc legea de evoluție similară sau a sistemului dinamic mecanic (de exemplu, câmpuri) de timp [1]. Evoluția unui sistem fizic este determinată în mod unic de ecuațiile ... ... Wikipedia
EQUATIONS - O ecuație este o relație matematică care exprimă egalitatea a două expresii algebrice. Dacă egalitatea este valabilă pentru orice valori admisibile ale celor necunoscuți care intră în ea, atunci se numește o identitate; de exemplu, relația formei ... ... Enciclopedia din Collier
Panta liniei - Panta liniei drepte a coeficientului de ecuații pe planul de coordonate care este numeric egală cu tangenta unghiului (cel mai mic constituent al rotației axei Ox la axa y) între direcția pozitivă a axei x și o anumită linie dreaptă [1] ... ... Wikipedia.
Ecuatii diferentiale - I Ecuatii diferentiale ale ecuatiei care contine functiile necunoscute, derivati ai diferitelor ordine si variabile independente. Teoria ecuațiilor diferențiale. a apărut la sfârșitul secolului al XVII-lea. sub influența necesităților mecanicii și a altor discipline ale științelor naturii, ... ... Enciclopedia Sovietică Mare
Ecuatii diferentiale - I Ecuatii diferentiale ale ecuatiei care contine functiile necunoscute, derivati ai diferitelor ordine si variabile independente. Teoria ecuațiilor diferențiale. a apărut la sfârșitul secolului al XVII-lea. sub influența necesităților mecanicii și a altor discipline ale științelor naturii, ... ... Enciclopedia Sovietică Mare
Direct - Acest termen are alte semnificații, vezi Direct (valori). Direcționați unul dintre conceptele de bază ale geometriei, adică nu are o definiție universală exactă. Cu o prezentare sistematică a geometriei, o linie dreaptă este de obicei luată ca una ... ... Wikipedia
Linie directă - Imaginea liniilor dintr-un sistem de coordonate dreptunghiulară Directează unul dintre conceptele de bază ale geometriei. Cu o prezentare sistematică a geometriei, o linie dreaptă este de obicei luată drept unul dintre conceptele inițiale, care este determinată doar indirect ... ... Wikipedia
Imagine directă a liniilor dintr-un sistem de coordonate dreptunghiulare Directează unul dintre conceptele de bază ale geometriei. Cu o expunere sistematică a geometriei liniei drepte este luată de obicei ca fiind unul dintre conceptele de bază, ceea ce a determinat doar indirect prin ... ... Wikipedia
Geometria Integral - Teoria invariant (în ceea ce privește grupurile mapările continue pe sine) pe seturi de măsuri constând din subvarietăților (de exemplu, linii, plane, convexe, suprafețe geodezice etc. manifolds conservare matematică Encyclopedia ... ......
- Sisteme canonice de două ecuații diferențiale. Anna Zhukova și Anatoly Perov. Ecuația lui Hill este bine cunoscută în teoria oscilațiilor. Una dintre cele mai importante și dificile sarcini în studiul ecuației Hill este problema durabilității și a stabilității sale în cazul în care este ... Citeste mai mult Vand pentru 4798 UAH (Ucraina numai)
- Set de mese. Geometrie. Gradul 9. 13 tabele + metodologie. Tabelele sunt tipărite pe un carton poligrafic gros cu o dimensiune de 680 x 980 mm. Kitul include o broșură cu indicații pentru profesor. Album educativ de 13 coli. Coordonate: ... Mai multe informații Cumpărați pentru 3016 руб
- Metode de ecuații integrale de graniță și elemente limită. Valentin Bazhenov. Monografia este o prezentare secvențială a unei noi metode numerice-analitice pentru rezolvarea problemelor dinamice ale mecanicii unui solid deformat. O opțiune directă este prezentată ... Mai multe informații Cumpărați pentru e-book