- dependența de magneziu. proprietăți (în sensul îngust - magnetizare) din direcția selectată din eșantion (magnet). Există dezacorduri. specii de M. a. Dependența magnetizării în direcția ei față de cristalografie. axele în cristale sunt numite. câmp magnetic cristalografic natural. În plus, M. a. pot apărea ca rezultat al deformărilor magnetoelastice, în prezența forțelor exterioare. sau int. (induse de câmpurile magnetice) și, de asemenea, din cauza anizotropiei formei eșantionului. M. a. afectează în mod substanțial procesele de inversare a magnetizării și magnetizării, structura domeniului magnetic și alte proprietăți ale magneților.
Energia este cristalografică. M. a. feromagnet magnetizat omogen poate fi scris în formă
unde sunt cosinele de direcție ale vectorului de magnetizare spontană M. și p. q. r sunt numere întregi. Coeficienți. Se numește par (p + q + r = 2n). constanta M. a. din ordinul n. (1) expansiunea în forma sferică este adesea folosită. armonici. Forma concretă a expresiei (1) și numărul coeficienților liniar independenți. Kpqr pentru un n dat sunt determinate complet de simetria cristalului. Constantele lui M. a. sunt funcții de exterior. parametrii: temperatura T, presiunea P și așa mai departe.
Rezultă din (1) că are valori minime și maxime pentru anumite valori. Direcțiile corespunzătoare sunt numite axe de magnetizare ușoară (OLD) și magnetizare dificilă. În absența unor situații externe. magnet. câmpul H, vectorul magnetizării spontane M (în interiorul domeniului) este direcționat de-a lungul HLN. În câmpul H, se întoarce, apropiindu-se direcția câmpului cu creșterea mărimii acestuia. Critice. Valorile lui H = H A, pentru care M este setat în H pentru magnetizare în direcții dificile, domenii de anizotropie. Valorile lui H A sunt legate de constantele lui M. a. Deci, pentru un cristal cubic. sinteze cu magnetizare de-a lungul axei [110] și, de asemenea, pentru cristale de syngene hexagonale HA = 2K / M. Curbele tipice de magnetizare pentru un singur cristal de Fe cu cubic centrat pe corp. sunt prezentate în Fig. 1.
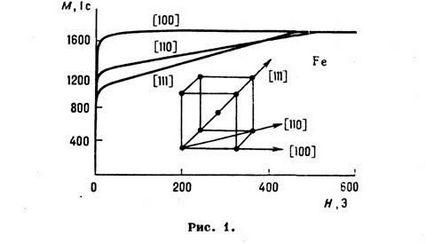
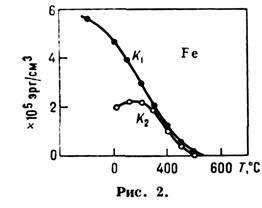
Constantele lui M. a. poate fi determinată din experiment. date: 1) aria curbelor de magnetizare pentru cristalele diferite direcții; 2) din măsurarea cuplurilor în anisometrul magnetic; 3) conform legii de aproximare a unui magnet la starea unui magnet. saturație (în policristal); 4) privind frecvența rezonanței feromagnetice. În unele cazuri (metale pământuri rare), se poate folosi conexiunea dintre constantele lui M. a. cu o anisotropie de paramagn. sensibilitate. Valorile K n sunt determinate pentru majoritatea magnonilor. materiale într-o gamă largă de temperaturi. În Fig. 2 avem K 1 (T) și K 2 (T) pentru Fe [în contrast cu definiția (1), numerotarea constantelor lui M. a. aici este dat în ordinea succesiunii lor, fără a lua în considerare constantele care dispar din condițiile de simetrie]. M. a. în feromagneți, antiferromagneți și feromagneți slabi (vezi ferimagnetismul, ferromagnetism slab) este de obicei mai complex decât în feromagneți.
Teoretic. cercetare M. a. vizează stabilirea principiilor fundamentale. microscopia, mecanismele de anizotropie și determinarea valorilor și a dependenței de temperatură a coeficientului. La n. Din punctul de vedere al naturii M. a. toți magneții sunt împărțiți în două tipuri: spin și orbital. Printre acestea se numără magneții bazați pe elemente de tranziție d (grupuri Fe), pe al doilea - panglici 4f de pământuri rare. Printre magneții grupului de uraniu se numără reprezentanți ai ambelor tipuri. În magneții d-spin, momentele orbitale ale electronilor L sunt aproape înghețați (vezi "Înghețarea" momentului unghiular orbital), astfel încât valorile cuantice- Miercuri valori și mag. momentul atomilor (ionilor) este determinat de magnitudinea spinării lor. Spinurile S "nu simt" anizotropia cristalului. M. a. apare datorită dezghețării parțiale a momentelor L prin interacțiunea cnun-ohrmal (PSB) cu energie (- constantă PSB). În același timp, micul moment de dezghețare l este orientat de-a lungul OLN, orientând, la rândul său, momentul total de rotire datorat PSB-ului. Energia lui M. a. pentru acest caz (anisotropia uniaxală), unde este diferența dintre energiile electronilor în stări pentru care elementul matricei L este nenul. Astfel. M. a. este rezultatul acțiunii combinate a unui câmp intracristalin anizotrop și a interacțiunii spin-orbită.
F. Bloch și G. Gentile (1931), iar apoi J. Van Vleck (1937) au considerat M. a. în modelul de rotiri localizate. NS Akulov (1936) pentru pui. cristale și K. Zener (S. Zener, 1954) c. mai general prin medierea dependenței energiei lui M. a. de la abaterile magiei. moment în câmpul de cristal, am obținut dependența de temperatură a K n (în expansiune în raport cu armonicile sferice):
unde M este magnetizarea spontană. Formula (2) a fost apoi obținută în pl. (inclusiv în cadrul teoriei undelor de spin), dar acordul său cu experimentul este, în unele cazuri, nesatisfăcător. Deci, de exemplu. În metale, se observă adesea schimbări ale semnului K n (T). Există dezacorduri. încearcă să îmbunătățească teoria (în special, ținând seama de expansiunea termică a magnetului), dar Das. Motivul acordului slab între teorie și experiment este aparent legat de inaplicabilitatea modelului de rotire a localizării la magnetul benzii (vezi magnetismul zonei).
În d-metale, cantitatea (m, m 'este numărul de sub-benzi degenerate și k este quasimomentul electronului). Estimările nu sunt foarte precise. Când erg, erg este erg. Astfel. erg, unde este energia momentului dezghețat în intracristalină. câmp. Magnetizarea în acest caz se datorează deviației lui S de la OLN la măsura raportului. În acest caz, l practic nu se abate datorită valorii mari. La E, magnetizarea în rotație este saturată. Calculele f-tionului pentru d-metale (EI Kondorskii, 1971) au arătat o dependență puternică de M. a. din detaliile structurii de bandă a magnetului.
În orbitalul 4 / -magnete, a. este determinată de energia totală a momentelor atomice J = L + S în stare intracristalină. câmp. Energia SOV în acest caz este mare. (spre deosebire de d-magneturile), astfel încât atunci când se produce magnetizarea, vectorul J se rotește ca un întreg întreg, iar constantele M. a. sunt determinate de energia momentelor J în starea intracristalină. câmp. Astfel, pentru cristalele uniaxiale
unde este coeficientul. Stevens, rf este raza f-shell-ului, este sarcina efectivă în, c și a sunt parametrii lattice. Formula (3) corespunde anizotropiei cu un singur ion și este de acord în mod satisfăcător cu experimentul atât în ordinea mărimii (K1
10 erg / cm3) și dependența (în ceea ce privește) numărul elementului din seria de metale pământuri rare (K1 inversează semnul între Ho și Er, Nd și Pm, așa cum se observă experimental).
În plus față de contribuția unică a ionului (3) la energia câmpului magnetic. există și așa-numitele. contribuțiile de două ioni datorate interacțiunii de schimb anizotropic a magnetului. ionelor și interacțiunea dipol-dipol. Determinarea valorii acestor contribuții este posibilă prin concentrarea. în aliaje. Experimente existente. datele indică predominant caracterul unic al MA. în magneți 4f.
Valoarea mare a a. în elementele de pământuri rare este crucială pentru crearea unui magnet tare record. materiale (cum ar fi SmCo5), având o specificație tehnică largă. cerere.
Valori mari ale constantelor MA. sunt de asemenea observate în anumiți compuși de actinidă, de exemplu, în US erg / cm3 (vezi materiale magnetice actinide).
REFERINȚE Turov, EA, Proprietăți fizice ale cristalelor ordonate magnetic, M. 1963; Berdyshev AA Introducere în teoria cuantică a feromagnetismului, Partea 3, Sverdlovsk, 1970; Vonsovskii SV Magnetism, M. 1971; Lesnik AG Anizotropia magnetică indusă. K. 1970; Kondorskii EI, Teoria zonelor magnetismului, partea 1-2, M. 1976-77. Yu, P. Irkhin.