Când fazele receptoarelor electrice sunt conectate la un triunghi, fiecare fază va fi conectată la două fire de linie, după cum se arată în figura de mai jos:
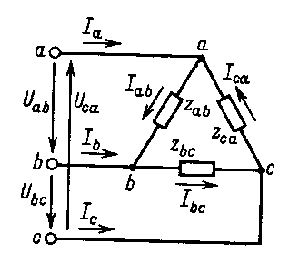
Prin urmare, cu acest tip de conexiune, înapoi la stea. indiferent de natura și valoarea rezistenței receptorului, fiecare tensiune de fază va fi egală cu cea liniară, adică UF = UL. Dacă nu luăm în considerare rezistența conductorilor de fază, putem presupune că tensiunea sursei și receptorul de energie electrică sunt egale.
Pe baza schemelor și formulele de mai sus se poate concluziona că faza de compus receptoare de energie electrică în triunghiul trebuie aplicat atunci când fiecare fază a două faze sau consumator trifazat de energie electrică este calculată în rețeaua de tensiune de linie.
Spre deosebire de o conexiune în stea, unde curenții de fază și de linie sunt egali, nu vor fi egali când sunt conectați printr-un triunghi. Aplicând prima lege a lui Kirchhoff la punctele nodurilor a, b, c, obținem relația dintre curenții fază și liniar:
Având vectori de curenți de fază, folosind această relație, nu este dificil să se construiască vectori de curent liniar.
Încărcare simetrică la conectarea receptoarelor într-un triunghi
Pentru orice fază, se pot aplica formule valabile pentru circuitele monofazate:
Evident, cu o sarcină simetrică:
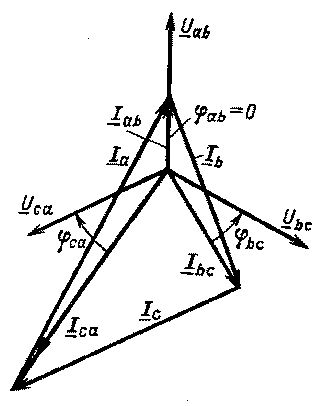
Diagrama vectorială a tensiunilor și curenților fază (liniari) cu sarcină simetrică inductivă activă este prezentată mai jos:
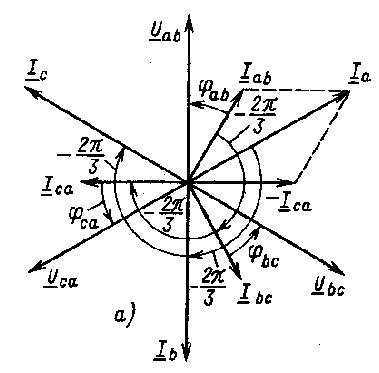
În conformitate cu formula (1), vectorii de curent liniar au fost construiți. De asemenea, merită acordată atenție faptului că atunci când se construiește diagrame vectoriale pentru conectarea unui triunghi, vectorul de tensiune liniară Uab este considerat a fi direcționat vertical în sus.
Vectorii de curenți liniare sunt adesea descriși ca vectori de fază de conectare, așa cum se arată în figura b):
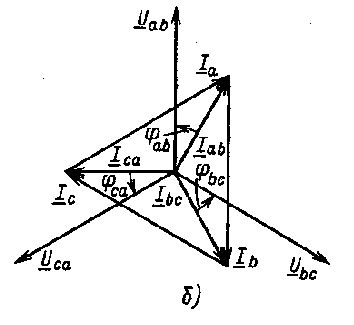
Pe baza acestei diagrame vectoriale, putem scrie :. Aceeași relație este valabilă și pentru alte faze. Pe baza acestui fapt, este posibil să se deducă o formulă pentru relația dintre fază și curentul liniar pentru conectarea fazelor consumatorilor cu un triunghi sub o sarcină simetrică.
O rețea de trei faze are tensiunea liniei UL = 220 V. Pentru conectarea la consumatorii de energie cu trei faze, cu o tensiune de fază de 220 V și cuprinzând înseriată activă Rf = 8,65 ohmi și xf inductiv = 5 ohmi rezistență.
Deoarece tensiunile liniare și de fază în acest caz vor fi egale, vom alege modul de conectare a înfășurărilor consumatorului într-un triunghi.
Curenții liniare și de fază, precum și rezistențele totale de fază vor fi egale cu:
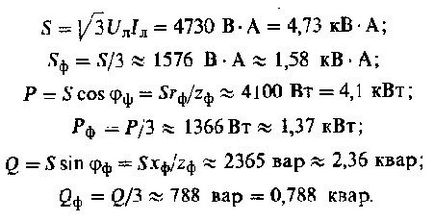
Diagramele vectoriale sunt date mai sus.
Sarcină neechilibrată la conectarea receptoarelor într-un triunghi
În cazul rezistenței fazei nesimetrice ca într-o conexiune stea, pentru conectarea la receptoarele electrice împărțite în trei grupe de aproximativ aceeași putere. Conectarea fiecărui grup se face la conductoare cu două faze, care au diferențe de fază:
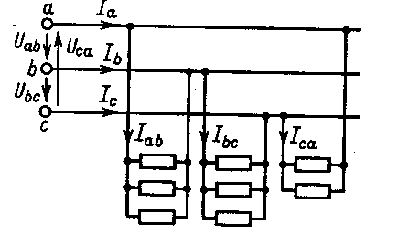
În cadrul fiecărui grup, receptoarele sunt conectate în paralel.
După înlocuirea rezistenței mai multor receptoare într-o singură fază cu un echivalent, obținem următoarea schemă:
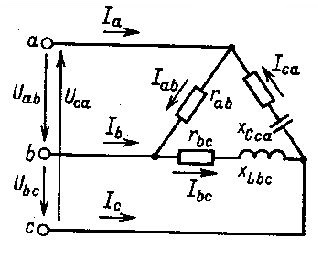
Unghiurile de forfecare dintre tensiune și curent, curenții de putere și de fază pot fi găsite în formula (2). În cazul unei sarcini asimetrice (în cazul nostru, circuitul este mai mare), puterile de fază, curenții și, de asemenea, unghiurile de deplasare (cos φ) nu vor fi egale. Diagrama vectorială pentru cazul în care faza ab are o sarcină activă, bc - activă-inductivă, ca-activ-capacitivă, este prezentată mai jos:
Pentru a determina puterea totală a tuturor fazelor, trebuie utilizată următoarea expresie:
Dana asimetric circuit electric încorporat în cadrul schemei de mai sus, cu următorii parametri: UL = 220, rab = 40 ohmi, xLbc = 10 ohmi DBD = 17,3 ohmi XCA = 5 ohmi rCca = 8,65 ohmi. Este necesar să se determine curenții liniare și de fază, precum și puterea.
Folosind expresia pentru a determina valorile complexe, primim:
Valorile complexe rezistența totală a fazelor: Zab = 40 ohmi, ZBS = 17.3 + J10 ohm ZBS = 8,65 - ohmi J5.
Valori complexe și eficiente ale curenților liniare și de fază:
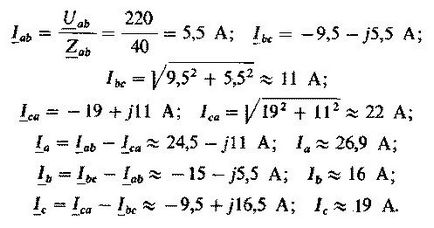
Este posibilă efectuarea unor calcule mai lungi fără a recurge la o metodă complexă:
Puterea totală activă și reactivă:
Unghiuri de forfecare între curenți și tensiuni:
Diagrama vectorială pentru un triunghi asimetric a fost dată mai sus.