Dacă o forță elastică Fy = -kX acționează asupra unui corp cu masa m, forța de frecare
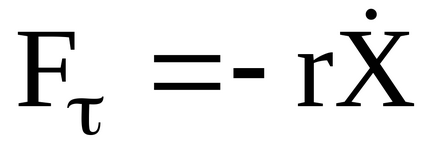
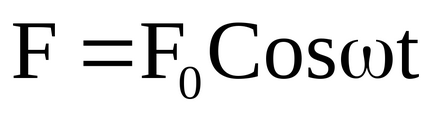
unde
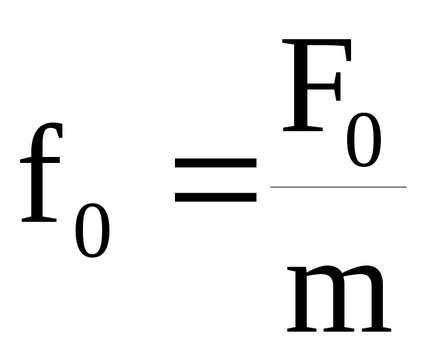
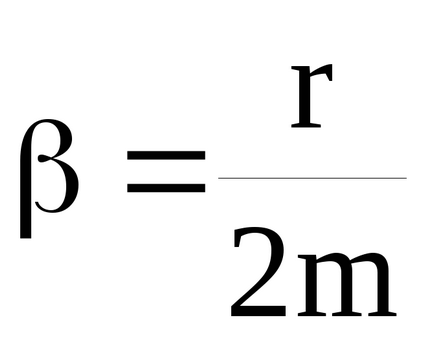
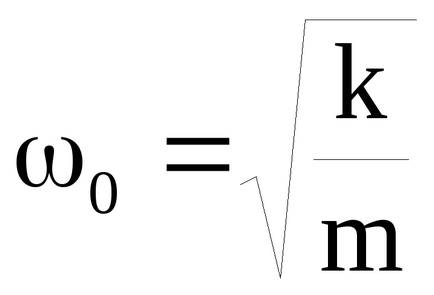
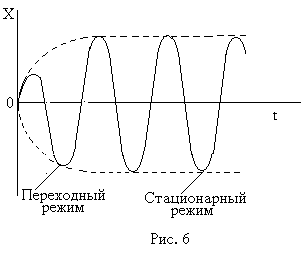
porii, până când toată energia furnizată de forța externă este folosită în întregime pentru a depăși frecarea, proporțională cu viteza. Prin urmare, se stabilește un echilibru la care suma energiilor cinetice și potențiale este constantă. Această condiție caracterizează starea staționară a sistemului.
Într-o astfel de stare mișcarea corpului va fi armonică cu o frecvență egală cu frecvența excitației externe, dar din cauza inerției corpului, oscilațiile sale vor fi schimbate în fază în raport cu valoarea instantanee a forței periodice externe:

Spre deosebire de vibrațiile libere, amplitudinea A și faza a oscilațiilor forțate
depinde nu de condițiile inițiale de mișcare, ci se determină numai prin proprietățile sistemului oscilant, prin amplitudinea și frecvența forței motrice:
Se poate observa că amplitudinea și deplasarea fazei depind de frecvența forței motrice (figurile 7 și 8).
O caracteristică caracteristică a oscilațiilor forțate este prezența unei rezonanțe. Fenomenul unei creșteri accentuate a amplitudinii oscilațiilor forțate ca frecvență a forței motrice se apropie de frecvența naturală a oscilațiilor libere neamplațate ale corpului ω0 se numește rezonanța mecanică. Amplitudinea oscilațiilor corpului la frecvența rezonantă
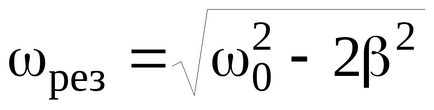
În ceea ce privește curbele de rezonanță (vezi figura 7), facem următoarele observații. Dacă ω → 0, toate curbele (vezi și (35)) ajung la aceeași valoare limită non-zero
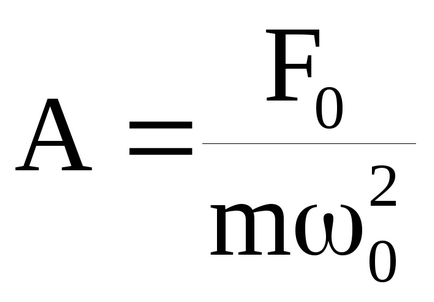
În condiția amortizării mici (β 2 << ω0 2), amplitudinea de rezonanță (vezi (37))
În această condiție, luăm raportul dintre părtinirea rezonanței și abaterea statică.
,
din care se poate observa că creșterea relativă a amplitudinii oscilațiilor la rezonanță este determinată de factorul Q al sistemului oscilator. Aici Q este, în esență, factorul de creștere a răspunsului
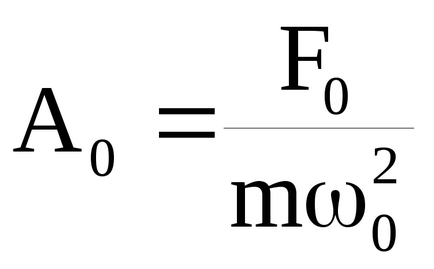
Această circumstanță determină importanța enormă a fenomenului de rezonanță în fizică și inginerie. Se folosește dacă doriți să amplificați oscilațiile, de exemplu, în acustică - pentru a îmbunătăți sunetul instrumentelor muzicale, în radiotehnică - pentru a izola semnalul dorit de la o varietate de alte care diferă în frecvență. Dacă rezonanța poate duce la o creștere nedorită a oscilațiilor, utilizați un sistem cu un Q mic.
Sursa forței periodice externe poate servi ca un al doilea sistem oscilator, asociat elastic cu primul. Ambele sisteme oscilante pot funcționa unul pe altul. Astfel, de exemplu, cazul a două penduluri cuplate (figura 9).
Sistemul poate efectua oscilații în fază (figura 9b) și antifază (figura 9c). Aceste oscilații sunt numite mod normal sau mod normal de oscilații și se caracterizează prin frecvența lor normală. Cu oscilații în fază ale deplasării pendulului în orice moment, X1 = X2. iar frecvența ω1 este exact aceeași cu frecvența unui singur pendul
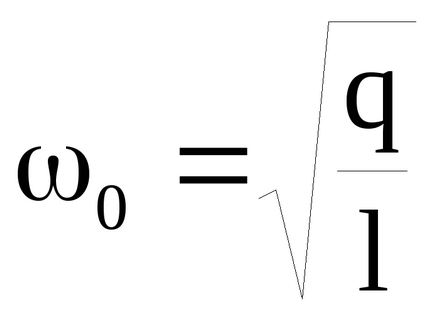
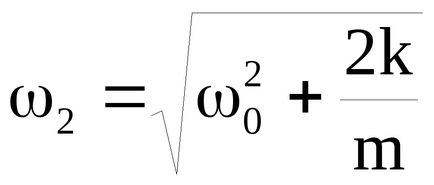
Orice stare a sistemului nostru legat, inclusiv deplasarea inițială X (Figura 9a), poate fi reprezentată ca suprapunere a două moduri normale:
Dacă transferăm sistemul în mișcare din starea inițială X, = 0,
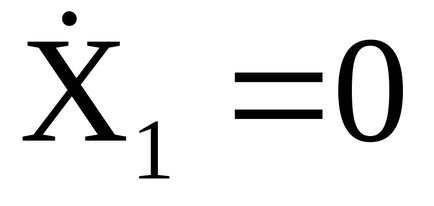
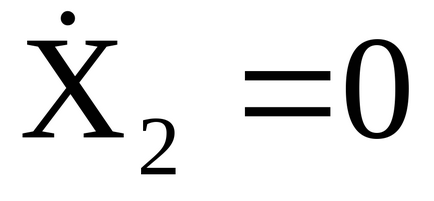
atunci deplasarea pendulului va fi descrisă de expresiile:
,
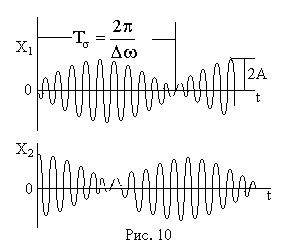
Frecvența de oscilație a pendulului este egală cu frecvența medie a celor două moduri normale
iar amplitudinea acestora variază în conformitate cu legea unui sinus sau a unui con cu o frecvență mai mică egală cu jumătate din diferența în frecvența modurilor normale
O schimbare lentă a amplitudinii cu o frecvență egală cu jumătate din diferența dintre frecvențele modurilor normale se numește "bătăi" a două oscilații cu frecvențe aproape identice. Frecvența "bătăilor" este egală cu diferența ω1 -ω2 frecvențe, (și nu jumătate din această diferență), deoarece amplitudinea maximă 2A este atinsă de două ori pe o perioadă corespunzătoare frecvenței
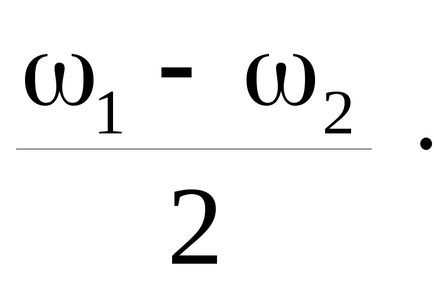
Prin urmare, perioada de bătăi este egală cu
Când bateți între pendul, energia este schimbată. Cu toate acestea, un schimb complet de energie este posibil numai atunci când ambele mase sunt aceleași și raportul (ω1 + ω2 / ω1 -ω2) este un număr întreg. Un punct important ar trebui remarcat: deși pendulurile individuale pot schimba energia, nu există schimb de energie între modurile normale.
Prezența unor astfel de sisteme oscilante, care interacționează una cu cealaltă și sunt capabile să transmită energia între ele, formează baza mișcării undelor.
Un corp de material oscilant, plasat într-un mediu elastic, poartă cu el și determină particulele mediului învecinat să vibreze. Datorită prezenței legăturilor elastice între particule, vibrațiile se propagă cu caracteristica de viteză a mediului dat pe tot mediul.
Procesul de propagare a oscilațiilor într-un mediu elastic este numit val. Există două tipuri principale de valuri: longitudinale și transversale. În valurile longitudinale, particulele mediei oscilează de-a lungul direcției de propagare a undelor, în timp ce în undele transversale sunt perpendiculare pe direcția de propagare a undelor. Nu în orice mediu elastic este posibil să propagați un val transversal. Un val elastic transversal este posibil numai în mediile în care are loc o deformare elastică de forfecare. De exemplu, în gaze și lichide se propagă numai undele elastice longitudinale (sunetul).
Locul geometric al punctelor mediei, până la care oscilația a atins momentul, se numește frontul valurilor. Partea frontală a valului separă o parte din spațiul deja implicat în procesul de undă, dintr-o zonă în care nu s-au produs încă vibrații. În funcție de forma frontului, undele se disting prin valuri plane, sferice, cilindrice etc.
Ecuația unei valuri plane propagând fără pierderi într-un mediu omogen are forma
unde ξ (X, t) este deplasarea particulelor mediei cu coordonata X din poziția de echilibru la momentul t, A este amplitudinea,
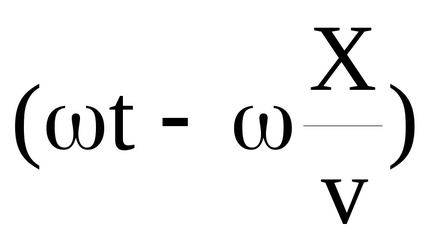
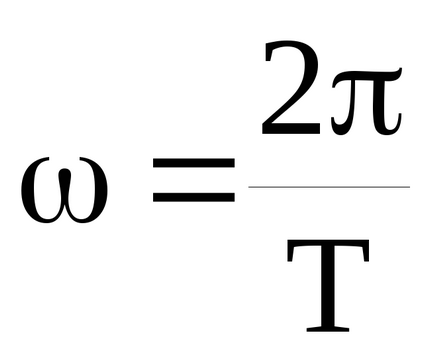
Lungimea de undă λ este distanța dintre punctele care oscilează cu diferența de fază 2π, cu alte cuvinte, lungimea de undă este calea traversată de orice fază a undelor într-o singură perioadă de oscilație:
viteză de fază; viteza de propagare a acestei faze:
Numărul de valuri - numărul de lungimi de undă care se potrivesc pe o lungime de 2 μ unități:
k = ω / v = 2π / λ. (45)
Substituind aceste notații în (42), ecuația unui val monocromatic care călătorește plane poate fi reprezentată în formă
Observăm că ecuația valurilor (46) prezintă periodicitate dublă în coordonate și timp. Într-adevăr, fazele oscilațiilor coincid când coordonatele se schimbă cu λ și când
schimbarea timpului cu T (perioadă). Prin urmare, nu este posibil să reprezentăm grafic un val în plan. Adesea, timpul t este fix, iar graficul deplasării lui ξ pe coordonata X este reprezentat pe grafic, adică distribuția instantanee a deplasărilor particulelor mediului în lungul direcției de propagare a undelor (figura 11). Diferența de fază Δφ a punctelor mediei depinde de distanța ΔX = X2 - X1 între aceste puncte
Dacă valul se propagă în direcția opusă lui X, atunci ecuația undelor înapoi este scrisă ca:
ξ (X, t) = ACos (ωt + kX). (48)
UMEILE STANDARD sunt rezultatul unui tip special de interferență a undelor. Ele se formează atunci când sunt aplicate două valuri de călătorie, propagându-se unul pe celălalt cu aceleași frecvențe și amplitudini.
Ecuațiile a două valuri plane propagând de-a lungul axei X în direcții opuse au forma:
Adăugând aceste ecuații prin formula sumă cosinus și ținând seama de faptul că k = 2π / λ, obținem ecuația valurilor în picioare
Factorul COS ωt arată că la punctele mediului există o oscilație cu aceeași frecvență ω cu amplitudine
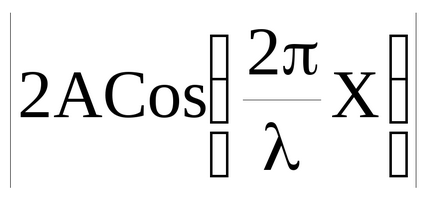
Amplitudinea oscilațiilor atinge o valoare maximă de 2A. Aceste puncte se numesc antinode. Din expresia (51) putem găsi coordonatele antinodelor:
La punctele unde
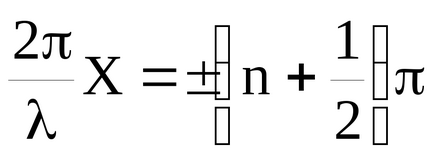
amplitudinea oscilațiilor dispare. Aceste puncte sunt numite noduri. Coordonatele nodurilor
P
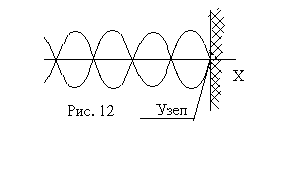
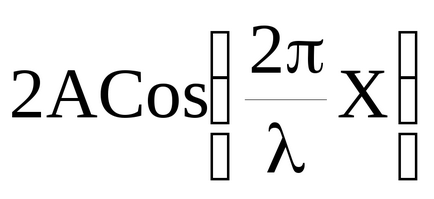
Distribuția nodurilor și antinodurilor într-un val în picioare depinde de condițiile care apar la interfața dintre cele două medii de la care are loc reflexia. Dacă reflexia valului este din mediul mai dens, atunci faza oscilațiilor la punctul de reflexie al undelor se schimbă spre opus sau, cum se spune, jumătate din valul este pierdut. Prin urmare, ca urmare a adăugării oscilațiilor cu direcții opuse, deplasarea la limită este zero, adică există un nod (Figura 12).

Într-un val în picioare nu există nici o deplasare de fază, nu există propagare de val, nu există transfer de energie, care este motivul pentru numele acestui tip de valuri.