Să considerăm dependența amplitudinii A a oscilațiilor forțate de frecvență. Oscilațiile mecanice și electromagnetice vor fi luate în considerare simultan, numind valoarea oscilantă fie deplasarea (x) a corpului oscilant din poziția de echilibru, fie sarcina (Q) a condensatorului.
Rezultă din (147.8) că amplitudinea A de deplasare (încărcare) are un maxim. Pentru a determina frecvența de rezonanță (cut - frecvența la care amplitudinea o prejudecată (încărcare) picuri - trebuie să găsiți maximul funcției (147,8), sau ceea ce este același lucru, diferențiindu cel puțin radicand expresie radicală a și egalează cu zero, obținem condiția. , definirea tăieturii:
Această egalitate este valabilă atunci când = 0, ±. în care numai o valoare pozitivă are un sens fizic. În consecință, frecvența de rezonanță
Fenomenul de creștere bruscă a amplitudinii de oscilație forțată atunci când frecvența forței motrice (îndemnând tensiune de curent alternativ de frecvență) la reducerea frecvenței de rezonanță numită (sau mecanică sau electrică). la <<значение рез практически совпадает с собственной частотой колебательной системы. Подставляя (148.1) в формулу (147.8), получим
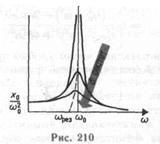
În Fig. 210 prezintă dependența amplitudinii oscilațiilor forțate de frecvența pentru diferite valori. De la (148.1) și (148.2) rezultă că cele mai mici. cea mai mare și cea dreaptă este cea a curbei date. În cazul în care. atunci toate curbele (a se vedea și (147.8)) ajung la aceeași valoare limită. așa-numita abatere statică. În cazul oscilațiilor mecanice. în cazul electromagnetice. Dacă toate curbele asimptotice tind să fie zero. Setul redus de curbe se numește curbele de rezonanță.
Rezultă din (148.2) că pentru atenuarea mică ( <<) резонансная амплитуда смещения (заряда)
unde Q este factorul de calitate al sistemului vibrațional (vezi (146.8)), este deviația statică considerată mai sus. Rezultă că factorul de calitate Q caracterizează proprietățile rezonante ale sistemului oscilator: cu cât Q este mai mare, cu atât este mai mare. În Fig. 211 prezintă curbele de rezonanță pentru amplitudinea vitezei (curentului), amplitudinea vitezei (curentului)
este maxim pentru re = și egal cu. adică, cu cât este mai mare coeficientul de amortizare. cu cât este mai mică curba de rezonanță.
Formulele ce utilizează (142,2) (146.10) și (143.4) (146.11), constatăm că amplitudinea vitezei la rezonanță mecanică este (. Și amplitudinea curentului electric în timpul rezonanță
Din expresia tg = 2 (a se vedea (147.9).) Rezultă că nu în cazul în care există o amortizare în sistem, (= 0), numai în acest caz, oscilație și forța motrice (tensiune de curent alternativ aplicată) au aceeași fază; în toate celelalte cazuri.
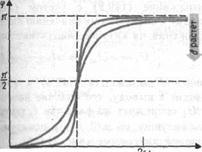
Dependența v pentru coeficienți diferiți este prezentată grafic în Fig. 212, din care rezultă că atunci când se face schimbarea, schimbarea de fază se schimbă. Rezultă din (147.9) că pentru = 0 = 0 și pentru = independent de valoarea coeficientului de amortizare. adică, forța (tensiunea) este înaintea oscilației în fază. Cu o creștere suplimentară a trecerii de fază, trecerea de fază crește de asemenea cu >>. și anume Faza oscilațiilor este aproape opusă fazei forței externe (tensiune alternativă). Familia de curbe prezentată în Fig. 212, se numește curbe de rezonanță de fază.
Fenomenele de rezonanță pot fi atât dăunătoare, cât și utile. De exemplu, în mașini pentru construcții și diferite tipuri de facilități necesare pentru frecvența naturală a acestora nu coincide cu frecvența posibilelor influențe externe, în caz contrar orice vibrație care poate provoca daune grave. Pe de altă parte, prezența unei rezonanțe face posibilă detectarea oscilațiilor chiar foarte slabe dacă frecvența lor coincide cu frecvența naturală a dispozitivului. Deci, ingineria radio, acustica aplicata, ingineria electrica folosesc fenomenul de rezonanta.