Conceptul de conectare a grafurilor aparține unuia dintre cele mai importante concepte ale teoriei grafurilor.
Două vârfuri arbitrare xi. xj X din graficul G = (X, U) se spune că sunt conectate. dacă există o rută 5 în care vârfurile xi. xj va fi terminală. Se spune că un grafic este conectat. dacă sunt conectate oricare două dintre vârfurile sale, adică 2 noduri sunt unite de un lanț simplu. În caz contrar, graficul nu este conectat, ci fiecare dintre subgrafurile sale conectate G1. G2, ..., Ge este numit componentă conectată.
Din definiția conexiunii rezultă că:
într-un grafic conectat, vertexul xi este legat de sine (reflexivitate);
dacă vârful xi este conectat cu vârful xj. atunci xj este legat de xi (simetrie);
din care rezultă că relația de legătură este o relație de echivalență.
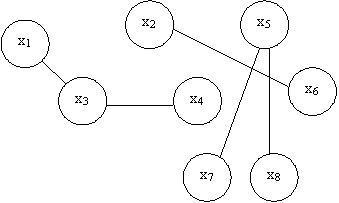
În acest caz, setul de noduri de graf G = (X, U), care simulează circuitul poate fi rupt în clase disjuncte Xi. iar marginile graficului vor conecta numai vârfurile din interiorul acestor clase. Numărul de componente care alcătuiesc un grafic este numit gradul de conectare. Un grafic conectat constă dintr-o componentă conectată. Exemple de grafice constând din mai multe componente de conectivitate sunt prezentate în Figura 7.15.
Una dintre caracteristicile grafurilor conectate este numărul de margini dintr-un grafic cu n noduri și un număr dat k al componentelor de conectivitate. Numărul de margini satisface inegalitatea:
n - k m (n - k) (n - k - 1) / 2
Este conectat un grafic cu n noduri care conțin mai mult de (n-1) (n-2) / 2 muchii.