Sarcina calculului forței implică determinarea tuturor forțelor și momentelor perechilor de forțe care sunt atașate la fiecare legătură individuală a mecanismului. Aceste forțe sau momente trebuie cunoscute, de exemplu, pentru a calcula puterea legăturilor individuale ale mecanismului sau ale părților componente ale acestuia.
Pentru ca mecanismul este în echilibru sub influența forțelor externe, la una dintre legăturile aceasta trebuie să fie însoțită de o forță de echilibrare sau o pereche de echilibrare a forțelor, caracterizată prin cuplul - ecuație, depășește momentul. Această forță sau moment este în general considerată a fi aplicată unităților de acționare care fie primește energia necesară pentru blană de mișcare-INSM, din exterior, așa cum este cazul în mecanismele de mașini de lucru, sau dă, așa cum este cazul în mecanismele motorii.
Dacă sarcina inerțială a legăturilor nu este inclusă în numărul forțelor externe cunoscute în calculul forței mecanismului, atunci calculul forței mecanismului este numit static. Dacă, în calculul forței mecanismului, sarcina inerțială a legăturilor intră în numărul de forțe externe cunoscute aplicate legăturilor sale, atunci calculul forței mecanismului se numește kinetostatic. Pentru ao conduce, trebuie să cunoaștem legea mișcării legăturii de conducere pentru a putea determina sarcina inerțială a legăturilor.
Calculul puterii include. a) determinarea reacțiilor în perechile cinematice ale mecanismului, b) găsirea forței sau momentului de contrabalansare. Se produce în următoarea secvență.
1. Toate forțele externe aplicate pe legăturile mecanismului sunt determinate, a căror acțiune este necesară pentru a găsi reacțiile în perechile cinematice ale mecanismului.
2. Se determină punctul de aplicare și direcția (linia de acțiune) a forței de echilibrare sau.
3. Calculul puterii fiecărui grup de Assur în ordinea formulei inverse a structurii mecanismului.
4. În concluzie, se calculează puterea liniei de conducere.
Problemele sunt de obicei rezolvate folosind metoda grafic-analitică, folosind ecuațiile de echilibru ale întregului grup sau legăturile sale individuale sub forma
Printre forțele și momentele implicate în aceste ecuații. reacțiile și momentele de reacție în perechile cinematice ale grupului sunt incluse.
Bazat pe primul tip de ecuații vectoriale sunt construite poligoane forțe care sunt numite forțe de plan de grup fiind situat într-o reacție de grup extern în primul rând sunt perechile cinematice, iar apoi, în condițiile interne de echilibru a vaporilor pentru un grup de unități, luate separat.
Pentru reacțiile care apar între elementele perechilor cinematice, sunt acceptate următoarele notații: reacția de la legătura k la legătura l este denumită Rkl, reacția de la legătura l cu legătura k este denumită Rlk, respectiv. Este evident că
Reacția este caracterizată de magnitudinea (modulul), direcția și punctul de aplicare.
Neglijând fricțiunea în perechile cinematice, putem observa următoarele.
În perechea rotativă, se determină magnitudinea și direcția reacției, deoarece punctul de aplicare coincide cu axa de rotație a perechii. În perechea în mișcare, se determină magnitudinea și punctul de aplicare al reacției, deoarece este cunoscut numai faptul că direcția de reacție a unei astfel de perechi este întotdeauna perpendiculară pe axa direcției sale.
Un exemplu de calcul al forței mecanismului.
Efectuați un calcul al forței poziției setate a mecanismului de ghidare a compresorului (Fig.43, a), dacă lungimile legăturilor sunt 1AB = 0,05 m, lBC = 0,2 m; pozițiile centrelor de masă ale legăturilor: S1 = A, lBS2 = 0,1 m, masa legăturilor: m1 = 0, m2 = 0,5 kg, m3 = 0,40 kg; momentul central al inerției barei de legătură VS-IS2 = 0,0018 kgm 2. Viteza unghiulară a manivelei AB este constantă și egală cu # 969; 1 = 80 secunde -1. Rezistența rezistenței utile este PC = 250 N, este opusă (a se vedea figura 42a, b) și trece prin punctul C; gravitatea tijei - G2 = m2 g = 0.5 * 10 = 5 N, gravitatea cursorului - G3 = m3 g = 0,4 * 10 = 4 N. Forța de echilibrare este aplicată perpendicular pe legătura 1 la punctul A.
Se determină: reacția în perechea cinematică de translație C, care este perpendiculară pe linia cursorului, reacția în perechea rotativă C; reacția în perechea rotativă B; reacție în perechea rotativă A și forța de echilibrare aplicată la legătura 1.
Soluția. 1. Toate forțele externe care acționează asupra legăturilor mecanismului sunt atribuite, astfel că această etapă de calcul este efectuată.
2. Forța de echilibrare RU este aplicată perpendicular pe legătura 1 în punctul său B.
3. Mecanismul conține doar un singur grup. constând din
din legăturile 2 și 3. Acest grup aparține clasei a doua a celui de-al doilea tip,
Formăm ecuațiile de echilibru pentru grup. Se descompune reacția în două componente: direcționat perpendicular pe linia BC și. direcționate de-a lungul liniei BC. Apoi suma geometrică a forțelor aplicate grupului (Fig.43, b) este
Ca a doua ecuație, ecuația = 0, care, atunci când este extinsă, ia forma
unde hG2 = 0,09 m este brațul forței G2 în raport cu punctul C (găsit conform desenului).
hFI2 = 0,07 m - umărul de forță PI2 față de punctul C (găsit prin desen).
Construim planul forțelor grupului (figura 43c) pe o scală # 956; P = 2 n / mm.
Ordinea de a construi suma vectorială este, în general, indiferentă, dar putem recomanda următoarele grupului asyrian dat: trasăm o linie paralelă cu BC. Aceasta va fi linia de actiune a fortei. Ne amana de la punctul arbitrar care se afla pe aceasta linie dreapta (Figura 43, c), forta in forma
segment (ab) = = = 27 mm, perpendicular pe punctul pryamoy.Ot b amâne putere ca interval (bc) = = 2,5 mm, de la un punct cu mai multă forță să amâne un segment (cd) = = = 60 mm. Din punctul d amâne vigoare în forma unei piese (de) = = = 44 mm. Mai departe de punctul e amâna vigoare în forma unei piese (ef) = = = 2 mm. Forța este amânată sub forma unui segment (fg) = = = 125 mm. Amânăm forțele în conformitate cu instrucțiunile din desenul grupului. Și în cele din urmă. din punctul g restaurare perpendicular (linia de acțiune a forței) până la intersecția cu linia de acțiune a punctului de forță rezultantă a începe vectorului k-. Segmentul (ka) în scară # 956; P dă reacția dorită. iar segmentul (gk) în aceeași scară este reacția, iar segmentul (kb) dă reacția dorită.
Pentru a găsi reacția, scriem condiția de echilibru a legăturii 2:
Din planul forțelor (Figura 43, c) se poate observa că segmentul (dk) pe o scară P corespunde reacției dorite. Reacția trebuie să treacă prin punctul C.
5) Calculul puterii liniei de ghidare 1 (Fig.43, d). La forța 1 se aplică forța = - (valoarea sa este determinată de planul forțelor (figura 7, c) de segmentul (kb), forța = (kb) # 956; P = 65 * 2 = 130 N, forța (reacția) aplicată la punctul A și forța de echilibrare RU. Aplicând perpendicular pe legătura 1 în punctul B. Deoarece suma momentelor relativ la punctul A al forțelor aplicate la legătura 1 este zero, găsim magnitudinea forței de contrabalansare RU
unde h21 (brațul forței) este situat sub desen (fig.43, d).
Condiția ca suma vectorilor forțelor aplicate la legătura 1 să fie zero va fi
Din aceasta găsim modulul reacției prin construirea unui triunghi de forță vectorial (Figura 43, d): R01 = (bc) # 956; P (H).
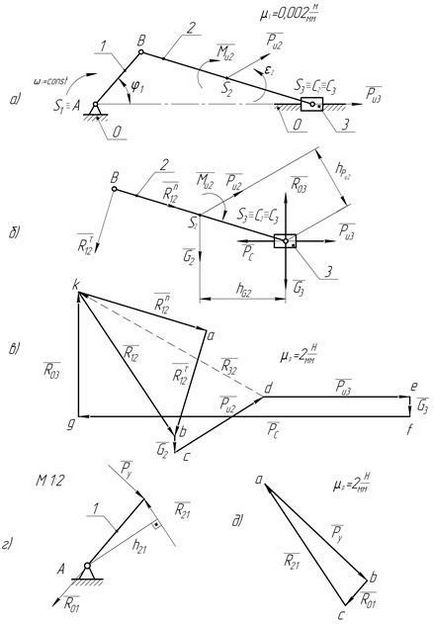
Fig.43. Calculul puterii mecanismului glisorului-manivelă al compresorului. a) poziția mecanismului; b) un grup structural cu forțe aplicate; c) planul forțelor.
După determinarea valorii (Mu) a momentului perechii forței de echilibrare, se poate găsi puterea motorului necesară conducerii mașinii. Pentru a face acest lucru, trebuie să știți (# 969; 1) viteza unghiulară a manivelei 1.