Formula Bernoulli este convenabilă pentru calcule numai cu un număr relativ mic de teste. Pentru valori mari, este incomod să utilizați această formulă. Cel mai des în aceste cazuri utilizați formula Poisson. Această formulă este determinată de teorema Poisson.
Teorema. Dacă probabilitatea p de apariție a evenimentului A în fiecare test este constantă și mică și numărul de încercări independente n este suficient de mare, atunci probabilitatea apariției evenimentului A este exact egală cu aproximativ egală cu
Dovada. Fie probabilitatea apariției evenimentului A într-un test P și numărul de probe independente n. Indicăm asta. Locație. Substituim această expresie în formula lui Bernoulli:
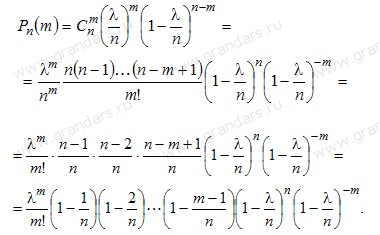
Pentru suficient de mari. n. și relativ mici. m. Toate parantezele, cu excepția celui penultim, pot fi considerate egale cu unul, adică
Având în vedere că este suficient de mare, partea dreaptă a acestei expresii poate fi luată în considerare când. și anume găsiți limita
Un exemplu. La întreprindere, au fost produse și trimise clienților 100.000 de sticle de bere. Probabilitatea ca sticla să fie un pic este de 0,0001. Găsiți probabilitatea că vor fi exact trei și exact cinci sticle sparte în expediția trimisă.
Dată: n = 100000, p = 0,0001, m = 3 (m = 5).
Folosim formula Poisson