Suma a doi vectori \ (\ mathbf \) și \ (\ mathbf \) este numit un vector al treilea \ (\ mathbf \), extrase din \ (\ mathbf \) pentru a termina \ (\ mathbf \), dacă este începutul vectorului \ (\ mathbf \) coincide cu sfârșitul vectorului \ (\ mathbf \). Adăugarea de vectori se face prin regula unui triunghi sau prin regula unei paralelograme.
\ (\ mathbf = \ mathbf + \ mathbf \)
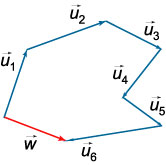
Suma mai multor vectori \ (\ mathbf \) \ (\ mathbf \) \ (\ mathbf, \; \ ldots \) este vectorul \ (\ mathbf \), adiția succesivă rezultantă a vectorilor de date. O astfel de operație se realizează prin regula unui poligon.
\ (\ mathbf = \ mathbf + \ mathbf + \ mathbf + \ ldots + \ mathbf \)
Legea comutativă a adăugării
\ (\ mathbf + \ mathbf = \ mathbf + \ mathbf \)
Legea asociativă de adăugare
\ (\ Stânga (+ \ mathbf> \ dreapta) + \ mathbf = \ mathbf + \ la stânga (+ \ mathbf> \ dreapta) \)
Suma vectorilor în coordonate
Când se adaugă cele două vectori, se adaugă coordonatele corespunzătoare.
\ (\ mathbf + \ mathbf = \ stânga (+, +, +> \ dreapta) \)
Diferența dintre doi vectori \ (\ mathbf \) și \ (\ mathbf \) este vectorul \ (\ mathbf \) sub condiția:
\ (\ mathbf = \ mathbf - \ mathbf \) dacă \ (\ mathbf + \ mathbf = \ mathbf \)
Diferența vectori \ (\ mathbf \) și \ (\ mathbf \) este suma vectorului \ (\ mathbf \) și vectorul \ opus (- \ mathbf \):
\ (\ mathbf - \ mathbf = \ mathbf + \ stânga (- \ mathbf \ right) \)
Diferența a doi vectori identici este egală cu vectorul zero.
\ (\ mathbf - \ mathbf = \ mathbf \)
Lungimea vectorului zero este egală cu zero:
\ (\ left | \ mathbf \ right | = 0 \)
Diferența vectorilor în coordonate
Când se scad două vectori, se scad și coordonatele corespunzătoare.
\ (\ mathbf - \ mathbf = \ stânga (-, -, -> \ dreapta) \)