
Subiect: Unificarea și intersecția decalajelor numerice
- pentru a introduce conceptul de intersecție și uniune de intervale numerice, pentru a stabili noțiunea de interval numeric, pentru a învăța să construiască decalaje numerice pe linia de coordonate.
- pentru a promova dezvoltarea de: memorie, vorbire, atenție, gândire logică.
- educa responsabilitatea, perseverența și voința de a atinge rezultatele finale.
Echipamente. tablă interactivă.
Metode. verbal, vizual, practic.
Concepte de bază. interval, segment, interval jumătate deschis, rază, fascicul deschis; intersecția și unirea lacunelor.
Tipul lecției: explicarea materialului nou.
Epigrafa lecției. Proverbul chinezesc spune:
"Ascult - uit,
Văd - îmi amintesc,
Fac - învăț.
I. Momentul organizatoric
Discursul introductiv al profesorului.
Astăzi avem mulți oaspeți,
Și le vom arăta toate cunoștințele,
Ce știm și ce trebuie să învățăm.
Vom face. desigur, sarcinile de rezolvat
Sarcini vă va ajuta să învățați mai bine.
Te obligă să muncești din greu.
Știința este persistentă și persistentă.
Păi, e timpul să începem
Aceste întrebări sunt răspuns de mine.
II. Actualizarea cunoștințelor de bază
1. Se efectuează un studiu privind materialul acoperit.
Toți li se oferă un card cu întrebări pe această temă
1. Ce se numește. diferența numerică?
2. Dacă inegalitățile sunt scrise în semne <или>, ei sunt chemați
a) Strict
c) nu sunt stricte
3. Dacă inegalitățile sunt scrise cu semne ≤ sau ≥, atunci ele sunt chemați
a) Strict
c) nu sunt stricte
4. Ce interval este numit. intervale?
a) soluția inegalității situată între punctele cu coordonate, a și in
c) soluția inegalității nu se află între punctele cu coordonate, ci în
5. Ce interval numeric este numit. segment?
a) soluția inegalității include numerele care arată intervalul numeric
c) soluția inegalității nu include cifrele care indică un interval numeric.
6. Cum desemnăm punctele pe linia de coordonate a căror coordonate nu sunt o soluție de inegalitate
a) picteaza punctul
c) un cerc mic
7. Cum desemnăm punctele pe o linie numerică a cărei coordonate sunt soluții de inegalitate
a) vopsiți punctele
c) nu vopsiți peste punct
8. Ce paranteze sunt folosite pentru a indica goluri numerice
a) paranteze
c) paranteze pătrate
c) rotund și pătrat
2. dictarea matematică.
1. Scrieți numere întregi în spațiu:
(a) [-5; 2] b) (-6; 4) c) [-7; 6) d) (-3; 4)
2. Înregistrați și desemnați aceste lacune numerice:
a) o secțiune de la 1 la 4
b) intervalul de la 1 la 4
c) o jumătate de interval de la 1 la 4, inclusiv 4
d) fascicul de la -∞ la 5
3. Înregistrați diferența sub forma unei inegalități:
4. Desenați un set de numere pe linia de coordonate care satisfac inegalitatea:
a) x ≥ 5 b) х ≤ 3 c) х> 7 d) х<-4 д) -4 <х<4
III. "Intersecția și unirea intervalelor numerice"
Două intervale numerice între ele se pot "intersecta", "uni" sau intersecția lor poate fi un set "gol". Intersecția a două seturi numerice poate fi: interval, jumătate de interval, segment.
[- 2; 4] ∩ [1; 6] = [1; 4]
Două intervale numerice nu se pot intersecta. Apoi intersecția intervalelor de numere
[-4; 1] ∩ [3; 7] = este un set gol.
Combinând două lacune numerice.
Fiecare număr în intervalul [-2; 6] poate să aparțină cel puțin uneia dintre intervale
[-2; 3] sau [1; 6] sau ambele goluri. Intervalul [-2; 6] se numește unirea intervalelor. Este notat ca: [-2; 3] U [1; 6] = [-2; 6]
IV. Lucrați pentru fixarea materialului
Sarcină. Desenați intervalele date pe linia de coordonate. Găsiți intersecția și unirea decalajelor. Notă:
Profesorul citează epigrafa la lecție și întreabă întrebarea: "Cum înțelegeți cuvintele epigrafului?
Elevii și oaspeții își exprimă opinia.
VII. Tema.
P. 226 Nr. 991 (3.4); 992 (3.4)

Tema lecției: "Unificarea și intersecția lacunelor numerice"

- pentru a introduce conceptul de intersecție și uniune de intervale numerice, pentru a stabili noțiunea de interval numeric, pentru a învăța să construiască decalaje numerice pe linia de coordonate.
- pentru a promova dezvoltarea de: memorie, vorbire, atenție, gândire logică.
- educa responsabilitatea, perseverența și voința de a atinge rezultatele finale.

Epigrafa lecției. "Ascult - uit, văd - îmi amintesc, o fac - învăț."

Repetarea materialului: 1. Ce se numește. diferența numerică?
Setul de numere dintre numerele a și b este numit intervalul numeric.

2. Dacă inegalitățile sunt scrise cu semne. ei sunt chemați
- a) stricte
- c) nu sunt stricte

3. Dacă inegalitățile sunt scrise cu semne ≤ sau ≥, atunci ele sunt chemați
- a) Strict
- c) nu sunt stricte

4. Ce interval este numit. intervale?
- a) soluția inegalității situată între punctele cu coordonate, a și in
- c) soluția inegalității nu se află între punctele cu coordonate, ci în

5. Ce interval numeric este numit. segment?
- a) soluția inegalității include numerele care arată intervalul numeric
- c) soluția inegalității nu include cifrele care indică un interval numeric.

6. Cum desemnăm punctele pe linia de coordonate a căror coordonate nu sunt o soluție de inegalitate
- a) picteaza punctul
- c) un cerc mic

7. Cum desemnăm punctele pe o linie numerică a cărei coordonate sunt soluții de inegalitate
- a) vopsiți punctele
- c) nu vopsiți peste punct

8. Ce paranteze sunt folosite pentru a indica goluri numerice
- a) paranteze
- c) paranteze pătrate
- c) rotund și pătrat

Notați întregi în spațiu:
- (a) [-5; 2] b) (-6; 4) c) [-7; 6) d) (-3; 4)

Notați și indicați aceste lacune numerice:
- a) un segment de la 1 la 4 b) un interval de la 1 la 4 c) o jumătate de interval de la 1 la 4, incluzând 4 g) o rază de la -0 la 5

Notați diferența sub forma unei inegalități:

Desenați un set de numere pe linia de coordonate care satisface inegalitatea:
- a) х ≥ 5 b) х ≤ 3 c) х 7 d) х
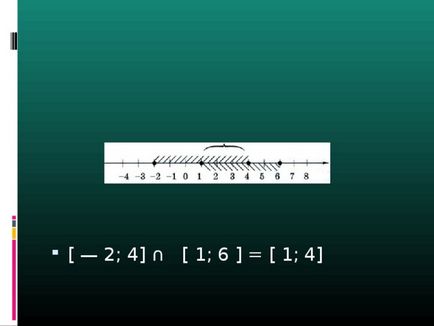
- [- 2; 4] ∩ [1; 6] = [1; 4]

- [-4; 1] ∩ [3; 7] = va fi un set gol

- [-2; 3] U [1; 6] = [-2; 6]

Desenați intervalele date pe linia de coordonate. Găsiți intersecția și unirea decalajelor. Notă:
- a) (1; 7) și (4; 9) b) [-5; 5] și [-3; 7] c) [-5; 0) și (2; 4) d) (-4; 1) și [5; 6]

