Prezentări înrudite






Diapozitive și text ale acestei prezentări

1. Este perechea numerelor (-1; 3) o soluție a sistemului de ecuații: 2x + y = 1 x-y = -4

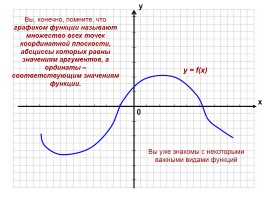
Ce înseamnă să soluționăm grafic sistemul de ecuații?
Algoritmul metodei grafice pentru rezolvarea unui sistem de două ecuații 1 2 3 4
x2 + y2 = 25 y = -x2 + 2x + 5

Ține minte două lucruri! Dacă nu există puncte de intersecție, atunci sistemul de soluții nu are; Coordonatele punctelor de intersecție sunt determinate aproximativ, deci soluțiile pot fi aproximative; Pentru a verifica acuratețea soluțiilor obținute, acestea trebuie înlocuite în ecuațiile sistemului!
Pentru a rezolva un sistem de două ecuații cu două necunoscute, trebuie: Construiți într-un sistem de coordonate graficele ecuațiilor care intră în sistem; Determinați coordonatele tuturor punctelor de intersecție ale grafurilor (dacă există); Coordonatele acestor puncte vor fi soluțiile sistemului.
mai departe
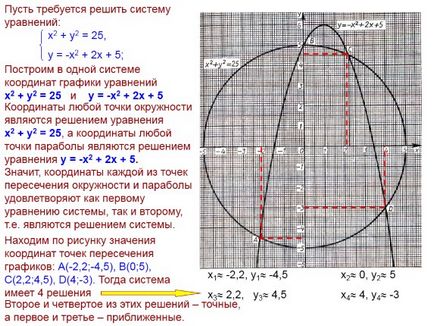
Construim într-un singur sistem de coordonate graficele ecuațiilor x2 + y2 = 25 și y = -x2 + 2x + s
Coordonatele oricărui punct al circumferinței sunt soluția ecuației x2 + y2 = 25, iar coordonatele orice punct al parabolei sunt soluții ale ecuației y = x2 + 2x + 5. Prin urmare, coordonatele fiecărui punct de intersecție al parabolei și circumferința satisface atât prima ecuație și al doilea, și anume Acestea sunt sistemul de soluție.
Citirea parcelelor de tragere valori de coordonate ale punctelor de intersecție: A (-2,2; -4,5), B (0, 5), C (2,2; 4,5), D (4, 3). Apoi, sistemul are 4 soluții
х1 -2,2, у1 -4,5 х2 0, у2 5 х3 2,2, у3 4,5 х4 4, у4 -3
A doua și a patra dintre aceste decizii sunt exacte, iar prima și a treia sunt aproximative.