<<Проекция вектора перемещения равна разности координат конца и начала
Două ambarcațiuni merg de-a lungul râului în direcții opuse și se întâlnesc în >>
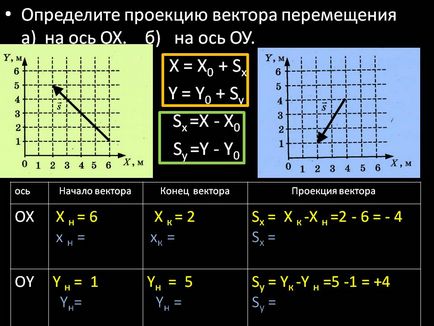
Determinați proiecția vectorului de deplasare a) pe axa OX. b) pe axa OU. X = X0 + Sx Y = Y0 + Sy Sx = X - X0Si = Y - Y0. Oh. XH = 6 x H =. Xk = 2 xk =. Sx = X k-X n = 2 - 6 = - 4 Sx =. Oy. Y n = 1 yn =. Yn = 5 yn =. Sy = yk-Y n = 5 -1 = +4 sy =. Axa. Începutul vectorului. Sfârșitul vectorului. Proiecția unui vector.
Slide 7 din prezentarea "Determinarea coordonatelor unui vector"
Dimensiuni: 720 x 540 pixeli, format. jpg. Pentru a descărca un diapozitiv gratuit pentru utilizare în lecție, faceți clic pe imagine cu butonul din dreapta al mouse-ului și faceți clic pe "Salvați imaginea ca". “. Descărcarea întregii prezentări "Definirea coordonatelor vectorului.ppt" poate fi în mărimea zip-arhivă 2806 KB.
Prezentări înrudite
"Mutarea clasei 9" - Mișcarea: rectilinie curbilină. Mutare -. Puzzle dezamăgit! Traiectoria este lat. următoarele. - Miscarea. Traiectoria -. Lungimea traiectoriei. Calea. - Segmente direcționate, care conectează poziția inițială și cea finală a corpului. Fun amuzant: Lungimea benzii de alergare la stadionul de 400m. Care erau urmele anvelopelor de pe șosea?
"Unghiul între vectori" - Unghiul dintre vectori. Produs scalar al vectorilor. Găsiți unghiurile dintre vectorii a și b? Proprietățile unui produs scalar? Cum să găsiți coordonatele segmentului de mijloc? Calculați cosinusul unghiului dintre linii. Găsiți unghiul dintre liniile BD și CD1. Analiza vizuală a sarcinilor din manual. Unghiul dintre liniile AB și CD.
"Produs scalar al unui vector" - Calculați produsul scalar al vectorilor: a) și b) și c) și. Găsiți produsul scalar al vectorilor (-1, 2) și (2, -1). Produsul scalar al vectorilor u este notat. Produs scalar al vectorilor. La ce valoare a t, vectorul este perpendicular pe vector. dacă (2, -1), (4, 3). Găsiți unghiul A al triunghiului cu vârfurile.
"Vectorii clasei a IX-a" - Regula poligonului. Regula de paralelogramă. Lungimea (modulul) vectorului. Vectorii collineare. Adăugarea de vectori. Vectorii collineare. Regula triunghiului. Vectorii. Sunt vectori egali?
"Probleme de rezolvare a vectorilor" - Exprimarea vectorilor AM, DA, CA, MB, CD prin vectorul a și vectorul b. BE. EC = 3. 1. K este mijlocul DC. Miercuri PD = 2,3; AK. KD = 1. 2. Exprimați vectorii CK, RK în termenii vectorilor a și b. Exprimați vectorii AE, AK, KE prin vectorii a și b. Aplicarea vectorilor la rezolvarea problemelor (partea 1). 1 Exprimați vectorii BC, CD, AC, OC, OA prin vectorii a și b.