Oscilațiile amortizate libere sunt acele oscilații ale căror amplitudine scade cu timpul din cauza pierderilor de energie în sistemul oscilator. Într-un circuit oscilator electric, energia este consumată pe căldură Joule și pe radiații electromagnetice.
Am considerat procesul de oscilații în buclă fără pierderi. Cu toate acestea, în circuitele reale, pierderile ireversibile de energie se produc întotdeauna pe încălzirea firelor și a dielectricilor, precum și pe radiații, ceea ce duce la o scădere treptată a amplitudinii oscilațiilor electrice sau, cum se spune, la atenuarea lor. Atunci când se calculează atenuarea unui circuit, se presupune că acesta are o rezistență concentrată care consumă aceeași cantitate de energie care este consumată în circuit pentru toate tipurile de pierderi.
Deoarece puterea pierderilor este proporțională cu rezistența activă a circuitului și puterea reactivă dezvoltată în elementele sale este proporțională cu reactanța lor, atunci bunătatea caracterizează și raportul dintre aceste capacități. Cu cât este mai mare factorul de calitate, cu atât oscilațiile libere în circuitele cu aceeași frecvență de degradare a oscilațiilor naturale sunt mai lent. Circuitele utilizate în radiotehnică de la bobine și condensatoare au de obicei un factor de calitate de 50 până la 300.
Energia primită de către antena transmițătorului de la circuitul oscilant se răspândește în spațiu sub formă de unde electromagnetice. Distanță. care trece un astfel de val într-un timp egal cu perioada de oscilații, se numește lungimea de undă # 955; În conformitate cu această definiție # 955; = # 965; T = # 965; / f, unde Viteza de propagare a undelor electromagnetice.
Pentru orice mediu
unde c este viteza propagării luminii în vid, 3,10 8 m / s, # 949; - relativ relativ dielectric și constante magnetice ale mediului.
Pentru aer poate fi luat în considerare # 965; = c și, prin urmare, dacă se substituie # 965; în m / s și f în MHz, atunci # 955; (m) = 300 / f (Mg).
Ecuație diferențială a oscilațiilor electrice amortizate într-o buclă cu rezistență electrică:
unde este coeficientul de atenuare, (aici este inductanța circuitului).
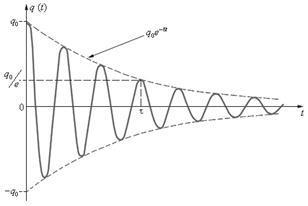
Ecuația oscilațiilor amortizate în cazul amortizării slabe () (figura 4.2):
unde este amplitudinea oscilațiilor amortizate ale sarcinii condensatorului; - amplitudinea inițială a oscilațiilor; - frecvența ciclică a oscilațiilor amortizate;
Timpul de relaxare este o perioadă de timp. în care amplitudinea oscilațiilor scade cu un factor de:
Timpul de relaxare este legat de coeficientul de atenuare prin relație
Reducerea logaritmică a amortizării oscilațiilor
unde este perioada oscilațiilor amortizate.
Formula care conectează scăderea logaritmică a oscilațiilor cu coeficientul de amortizare și perioada de oscilații amortizate:
30. Oscilații electromagnetice forțate.
Forțele oscilante sunt acele oscilații care apar atunci când există un efect extern în schimbare periodică.
Ecuația diferențială a oscilațiilor electrice forțate într-un circuit cu rezistență electrică. în prezența unui EMF de conducere. variind în conformitate cu legea armonică. unde este valoarea amplitudinii emf și a este frecvența ciclică a schimbării în emf (Figura 4.3):
unde este coeficientul de atenuare; Inductanța circuitului.
Fig. 4.3. Circuitul pentru observarea oscilațiilor electrice forțate
Ecuația oscilațiilor electrice forțate la starea de echilibru:
unde este diferența de fază a oscilațiilor de sarcină ale condensatorului și a EMF de antrenare a sursei de curent.
Amplitudinea oscilațiilor forțate la starea de echilibru a sarcinii condensatorului
Diferența de fază dintre oscilațiile de încărcare ale condensatorului și EMF-ul de antrenare a sursei de curent
Amplitudinea oscilațiilor forțate depinde de relația dintre frecvențele ciclice ale forței motrice și vibrațiile naturale. Frecvența rezonanței și amplitudinea rezonanței: