Oscilații oscilante libere în circuitul oscilator.
Circuitul oscilator este un circuit electric care constă din inductori conectați în serie L, un condensator de capacitate C și un rezistor de rezistență R.
Să considerăm etapele succesive ale procesului oscilator într-un circuit ideal cu rezistență neglijabilă (R = 0).
Condensatorul este preîncărcat, încărcările sunt încărcate. Apoi, în momentul inițial al timpului, se formează un câmp electric între plăcile, a căror energie este. Dacă condensatorul este închis inductorului, acesta va începe descărcarea și curentul va crește în timp. Energia câmpului electric al condensatorului scade, iar energia câmpului magnetic al bobinei crește. Curentul care crește cu timpul creează în bobină un câmp magnetic în creștere și, în consecință, un flux magnetic în creștere. Prin urmare, în conformitate cu legea lui Faraday de inducție electromagnetică, un curent de inducție apare în bobina, care este îndreptată spre curentul de descărcare a condensatorului și încetinește creșterea acestuia. Deoarece R = 0. atunci, conform legii conservării energiei, energia totală a sistemului rămâne constantă, deoarece pentru a încălzi energia nu este irosită:
Când curentul bobinei are o valoare maximă, condensatorul este complet descărcat. În acest moment, energia câmpului magnetic este maximă, iar câmpul electric este minim. Mai mult, după ce a atins valoarea maximă, curentul din circuit începe să scadă, astfel încât câmpul magnetic al bobinei scade. Acesta generează un curent de inducție care curge în aceeași direcție cu curentul de descărcare a condensatorului. Condensatorul este reîncărcat, încărcarea pe plăci atinge valoarea maximă, iar curentul în bobină este zero. Energia câmpului electric atinge un maxim, iar energia câmpului magnetic este minimă. Apoi procesele încep să curgă în direcția opusă.
Conform legii lui Ohm, - emf. auto-inductanța bobinei, - tensiunea pe condensator, - prin definiție.
Apoi. Soluția acestei ecuații, adică. taxa variază în funcție de o lege armonică cu o frecvență ciclică și cu o formulă de timp - Thomson.
Tensiunea pe condensator:
, unde este valoarea maximă a tensiunii pe condensator.
Puterea curentă în circuitul oscilator:
și anume Curentul variază în funcție de legea armonică și oscilațiile actuale depășesc tensiunea pe condensator cu / 2 în fază. Aceasta înseamnă că atunci când curentul atinge valoarea maximă, sarcina și tensiunea de pe condensator ajung la zero și invers.
Oscilații amortizate libere în circuitul oscilator.
Orice circuit oscilant real are o rezistență activă. Energia stocată în circuit este consumată treptat pentru încălzire, din cauza căreia oscilațiile libere sunt amortizate.
Legea lui Ohm pentru un circuit oscilant cu rezistență:
, - emf auto-inductanța bobinei, - tensiunea pe condensator, - prin definiție.
Indicăm asta. Apoi ecuația diferențială poate fi scrisă în formular.
Cu condiția ca, prin soluția acestei ecuații, să fie o expresie, adică încărcarea oscilațiilor se face cu frecvență.
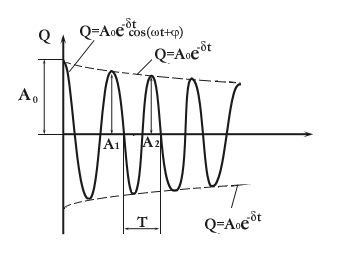
Tensiunea pe condensator:
Pentru că, atunci. Astfel, dacă amperajul rezistență circuitului conduce în fază de tensiune la bornele condensatorului cu mai mult de / 2.
Logaritmic decrement decrement :.
Pentru a compensa pierderile de energie în sistemul oscilant real și pentru a obține oscilații neconfirmate este necesar să acționăm asupra sistemului printr-o forță motrice exterioară care variază în funcție de timp în conformitate cu legea armonică.
În cazul unui circuit oscilant, sursa curentului cu emf joacă rolul forței motrice. . Conform legii lui Ohm:
Soluția ecuației diferențiale neomogene este:
Soluția generală a ecuației diferențiale omogene:
. După un timp suficient de lung, factorul devine mic și poate fi neglijat. Această soluție joacă un rol numai în stabilirea oscilațiilor.
O soluție particulară a ecuației diferențiale neomogene:
Oscilațiile forțate stabilite sunt determinate de expresie.
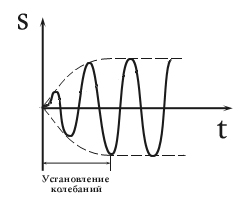
Puterea curentă în circuit :. Se scrie această expresie în forma: unde - schimbare de fază între tensiunea curentă și cea aplicată. atunci
În consecință, curentul înclină în fază de la tensiunea aplicată când, și avansează tensiunea atunci când.
Tensiunea pe rezistența activă :.
Tensiunea pe condensator: unde
Tensiunea pe bobină:
Astfel, tensiunea pe condensator rămâne în fază de la puterea curentă cu / 2. Tensiunea la bobină este în avans față de curent cu / 2. Tensiunea de rezistență este în fază cu curentul.
Arborele armonic poate fi specificat folosind un vector. Să luăm ca linia din care se măsoară faza inițială, axa curenților. Apoi, tensiunea pe rezistență, condensator și bobina poate fi reprezentată în diagramă. Tensiunea totală trebuie să fie egală cu tensiunea aplicată, deoarece conform legii lui Ohm. Prin urmare, în diagramă, tensiunea U este reprezentată de suma vectorilor.
Rezultă din formula că amplitudinea încărcării și tensiunii pe condensator are un maxim la frecvența îndelungată. Pentru a găsi frecvența maximului, trebuie să diferențiem amplitudinea amplitudinii în raport cu frecvența, apoi vom obține. Pentru curbele de rezonanță converg la un punct c.
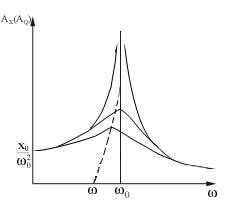
Amplitudinea intensității curente are o valoare rezonantă la. Prin urmare, frecvența rezonantă pentru puterea curentă coincide cu frecvența naturală a circuitului. Curbele de rezonanță pentru curentul I încep de la zero, deoarece la tensiune constantă, curentul staționar în circuitul cu condensatorul nu poate curge.
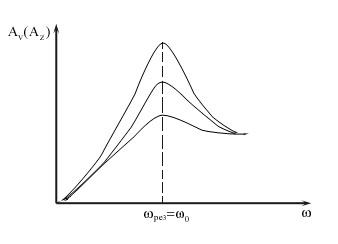
Rezultă din ecuațiile lui Maxwell că un câmp magnetic alternativ generează un câmp electric alternativ și un câmp electric alternativ generează un câmp magnetic alternativ. Ie campurile electrice și magnetice sunt legate în mod inextricabil între ele. Ele formează un singur câmp electromagnetic. Dacă un câmp electromagnetic alternativ este excitat prin încărcări oscilante, atunci în spațiul din jur va apărea o secvență de transformări mutuale ale câmpurilor electrice și magnetice propagatoare în spațiu de la un punct la altul. Acest proces va fi periodic în timp și în spațiu, fiind un val electromagnetic.
Arătăm că existența undelor electromagnetice rezultă din ecuațiile Maxwell:
În cazul unui mediu omogen neutru ( = 0) neconductor (j = 0) cu constante and , ecuațiile lui Maxwell pot fi rescrise:
Luăm rotorul din ambele părți ale ecuației (1):
Aici vom folosi relația și vom ține cont de asta. Conform (3), primul termen de exprimare (5) este egal cu zero. Prin urmare.
Modificarea ordinii de diferențiere în ceea ce privește coordonatele și timpul conduce la egalitate:
Folosind relația (2), obținem
În mod similar, putem obține o ecuație pentru vectorul H, luând rotorul din ecuația (2):
Ecuațiile (6) și (7) sunt inextricabil legate între ele, deoarece ele sunt obținute din ecuațiile Maxwell, care conțin atât E cât și H.
Ecuațiile - reprezintă ecuația valurilor și viteza de fază a undelor. Într-un vid. În mediul înconjurător. Ie c este viteza de propagare a undelor electromagnetice într-un vid este viteza limitatoare de propagare a undelor electromagnetice.
Luați în considerare un avion electromagnetic plan propagând într-un val neutru omogen ( = 0). mediul neconductor (j = 0) cu constantele și . Direcționăm axa x perpendicular pe suprafețele undei, adică vectorii E și H și componentele lor de-a lungul axelor de coordonate nu vor depinde de coordonatele y și z.
Apoi ecuațiile lui Maxwell pot fi scrise sub forma:
Astfel, u nu depinde de x.
Se scrie cea de-a X-a componentă a rotoarelor E și H:
Astfel, u nu depinde de x și de t. și anume Câmpul valurilor nu are componente pe axa x. și, în consecință, vectorii E și H sunt perpendiculați pe direcția de propagare a undelor. Aceasta înseamnă că undele electromagnetice sunt transversale.
Să presupunem că a fost inițial creat un câmp direcționat de-a lungul axei y. Conform ecuației Maxwell, acest câmp creează un câmp magnetic alternativ direcționat de-a lungul axei z. Conform unei alte ecuații Maxwell, acest câmp creează un câmp electric. Astfel, vectorii E și H sunt reciproc perpendiculari
Diferențierea primei ecuații cu privire la x. și înlocuind în a doua ecuație, obținem: u.
Soluția acestor ecuații este funcția:
, unde k este numărul de undă, 1 și 2 sunt fazele inițiale.
Înlocuim aceste expresii în ecuațiile și. Avem:
Pentru ca ecuațiile să fie satisfăcute, este necesar ca fazele inițiale să fie egale: 1 = 2. Înmulțim aceste două expresii. Astfel, oscilațiile vectorilor E și H apar în fază, iar amplitudinile vectorilor în fiecare moment al timpului sunt legate de relația :.
Proprietățile undelor electromagnetice:
1. Din ecuațiile Maxwell rezultă că vectorii puterii E și H ale câmpului electromagnetic satisfac ecuația de undă:
, unde este operatorul Laplace, v este viteza de fază.
2. Viteza de fază este determinată de expresia:, unde o și o sunt constantele electrice și magnetice, și sunt permeabilitățile electrice și magnetice ale mediului. În vid, viteza de propagare a undelor electromagnetice coincide cu viteza c. pentru că , atunci viteza de propagare a undelor electromagnetice în materie este întotdeauna mai mică decât viteza de propagare a undelor electromagnetice într-un vid.
Undele electromagnetice sunt transversale, adică vectorii intensității câmpului electric și magnetic E și H din val sunt perpendiculari reciproce și se află într-un plan perpendicular pe vectorul de viteză v al valului.
4. Vectorii E și H continuă să oscileze în aceleași faze, valorile instantanee ale E și H în orice punct sunt legate de
5. Ecuațiile valurilor sunt satisfăcute de undele monocromatice plane (valuri cu o frecvență strict definită):
, unde k este numărul de undă.
Energia undelor electromagnetice. Vectorul Umov-Poynting. Impulsul câmpului electromagnetic.
Densitatea energetică în vrac a undei electromagnetice este compusă din densitățile în vrac și wm ale câmpurilor electrice și magnetice:
Densitatea energetică a câmpurilor electrice și magnetice este aceeași în fiecare moment al timpului.
Dacă înmulțim densitatea energetică cu viteza de propagare a undelor în mediu, obținem modulul de densitate a fluxului de energie S = wv = EH. pentru că vectorii E și H sunt perpendiculați, atunci direcția vectorului coincide cu direcția transferului de energie. Vectorul densității de flux a energiei electromagnetice este numit vectorul Umov-Poynting: este direcționat spre propagarea undelor electromagnetice.
Absorbit în orice corp, un val electromagnetic informează acest corp de o anumită impuls, adică exercită presiune asupra lui. Experimentele lui Lebedev din 1908 dovedesc că lumina exercită o presiune asupra corpului.
Lăsați planul unde electromagnetică să cadă pe suprafața plană a unui corp slab conducător. Câmpul electric al unui val electromagnetic excită un curent de densitate în corp. Câmpul magnetic al valului acționează asupra curentului cu forța de amperi, care, pe unitatea de volum a corpului, este egală cu :. În consecință, un strat de suprafață cu suprafața unu și o grosime dl. impulsul este raportat :. În acest strat, energia este absorbită pe unitate de timp. Să împărțim aceste expresii între ele :. ()
În consecință, impulsul pe unitatea de volum a câmpului electromagnetic: Vectorul Umov-Poynting. Direcțiile vectorilor p și S coincid.
Scară de undă electromagnetică.
Undele electromagnetice acoperă o gamă largă de frecvențe. Dar ele diferă una de alta în modul în care sunt generate și în modul în care sunt înregistrate, precum și în proprietățile lor. Prin urmare, undele electromagnetice sunt împărțite în mai multe tipuri: unde radio, undele luminoase, radiația X și radiația . (vezi Tabelul 5 de la pagina 298 Trofimova TI Cus Physics).
DEFINIȚII DE BAZĂ ȘI LEGISLAȚIA OPTICELOR GEOMETRICE.
Lumina este un val electromagnetic. În cazul undei electromagnetice, vectorii E și H oscilează. După cum arată experiența, efectul diferit al luminii asupra materiei este tocmai vibrațiile vectorului electric. Prin urmare, vectorul intensității câmpului electric al unui val electromagnetic se numește vectorul de lumină. Modulul de amplitudine al vectorului de lumină este notat cu A.
Indicele absolut al refracției unui mediu este o cantitate egală cu raportul dintre viteza undelor electromagnetice în vid și viteza lor de fază într-un mediu :.
Liniile de-a lungul cărora se deplasează energia luminoasă sunt numite raze. Valoarea medie a timpului de densitate a fluxului de energie transmisă de un val de lumină se numește intensitatea luminii I la un anumit punct din spațiu. În consecință ,. . În consecință ,. Puteți scrie asta.
O sursă punctuală de lumină este o sursă a cărei dimensiuni pot fi neglijate în comparație cu obiectul iluminat de ea sau distanța față de ea.
Legea propagării luminii rectilinii. lumina într-un mediu optic omogen (mediu cu un indice de refracție constant) se propagă rectiliniu. Dovada acestei legi este prezența unei umbre cu o limită clară atunci când iluminează un obiect opac. Legea este spartă când lumina trece prin găuri mici.
Legea independenței grinzilor de lumină. efectul produs de un fascicul separat nu depinde de faptul dacă celelalte fascicule acționează simultan sau nu.
Dacă lumina cade pe interfața dintre două medii, atunci fasciculul incident se rupe în două - reflectat și refractat.
Legea reflexiei. raza incidentă, raza reflectată și perpendiculară restabilită la interfața celor două medii în punctul de incidență se află într-un plan, iar unghiul de incidență este egal cu unghiul de reflexie.
Legea refracției. ray, razele refractare și perpendiculare, restaurate la interfața a două medii la punctul de incidență, se află în același plan. Sinusul unghiului de incidență se referă la sinusul unghiului de refracție ca indice de refracție al celui de-al doilea mediu la indicele de refracție al primului mediu :.
Dacă lumina cade dintr-un mediu optic mai puțin dens spre un mediu dens mai dens, adică n1
Pe măsură ce unghiul de incidență crește, unghiul de refracție crește și el. La un unghi de incidență. unghiul de refracție este 2 = 90. Cu o creștere suplimentară a unghiului de incidență, raza refractată nu mai există și lumina este reflectată complet din interfața celor două medii. Pe măsură ce unghiul de incidență se apropie de limită, intensitatea razei refractare scade, iar raza reflectată crește. Pentru i = i, intensitatea razei refractare este zero, iar intensitatea reflectată este egală cu intensitatea razei incidente. Acest fenomen se numește fenomenul de reflecție totală.
Fenomenul reflexiei totale este folosit în prismele de reflecție totală. Indicele de refracție al sticlei este n = 1,5, prin urmare i prev = 42 0 (arcsin 1 / 1,5). Când lumina cade pe limita de sticlă-aer la i> ipr. atunci va exista o reflecție totală. Fasciculul poate fi rotit cu 90 °. Radiațiile pot fi înfășurate, puteți roti imaginea.
Fenomenul reflexiei totale este folosit în fibrele optice, care este un miez de lumină din sticlă, înconjurat de o carcasă de alt sticlă, cu un indice de refracție mai mic. Incidenta luminii de pe cap la unghiuri mai mari decât maximul, la interfața dintre miez și coajă, suferă o reflexie completă și se propagă numai în vena luminată.
Corpusculară și teoria valurilor de lumină.
Legile fundamentale ale opticii geometrice au fost cunoscute încă din timpul vechilor greci. Noțiunea de natură a luminii a fost transformată din secolele XVII-XIX. Până la sfârșitul secolului al XVII-lea au apărut două teorii ale luminii: corpuscul (Newton) și valul (Hooke și Huygens). Teoria corpusculară a descris bine interacțiunea dintre lumină și materie (împrăștiere, absorbție), iar teoria undelor a descris bine legile propagării luminii (difracție, interferență). O teorie poate descrie complet toate legile radiației, propagarea și absorbția luminii nu pot. În lumină, se manifestă dualismul valurilor corpusulare.