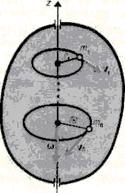
Considerăm că un corp absolut rigid (vezi § 1) se rotește în jurul axei fixe z. trecând prin el (figura 24). Mental vom rupe acest corp în volume mici cu masele elementare. situat la o distanță de axa de rotație. Atunci când corpul rigid se rotește în raport cu axa fixă, volumele sale elementare individuale descriu mase de cercuri de diferite raze și au viteze liniare diferite. Dar din moment ce avem în vedere un corp absolut rigid, viteza unghiulară de rotație a acestor volume este aceeași:
Energia cinetică a unui corp rotativ se găsește ca suma energiilor cinetice ale volumelor sale elementare:
Folosind expresia (17.1), obținem
unde este momentul inerției corpului în raport cu axa z. Astfel, energia cinetică a corpului rotativ
Din compararea formulei (17.2) cu expresia (12.1) pentru energia cinetică a unui corp care se mișcă translațional, rezultă că momentul inerției mișcării de rotație este o măsură a inerției corpului. Formula (17.2) este valabilă pentru un corp care se rotește în jurul unei axe fixe.
În cazul unei mișcări plane a unui corp, de exemplu, un cilindru care alunecă dintr-un plan înclinat fără alunecare, energia mișcării este compusă din energia mișcării de translație și energia de rotație:
unde m este masa corpului de rulare; - viteza centrului de masă a corpului; - momentul inerției corpului în raport cu axa care trece prin centrul său de masă; Viteza angulară a corpului.