Mișcarea progresivă (bp)
Lăsați corpul să se miște sub acțiunea forței. Lucrare elementară dA = Fsds = Fds. Aplicând a doua lege a lui Newton și determinând accelerația tangențială, obținem: Fs = mat = mdu / dt și mai departe: dA =. Acest rezultat indică faptul că lucrarea este transformată într-o creștere a unei anumite valori corespunzătoare unei anumite stări a corpului. Această cantitate se numește energia cinetică a corpului - Ec:
Energia cinetică poate fi exprimată în funcție de caracteristica de stare a corpului - momentul p = mv:
Energia cinetică a unui corp rotativ poate fi găsită ca suma energiilor cinetice ale tuturor punctelor sale: Ek =
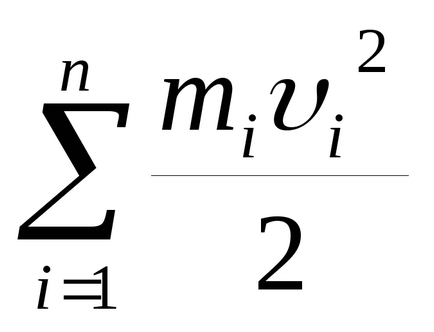
În practică, se întâmplă adesea rularea unui corp rigid - este o formă de mișcare atunci când toate punctele corpului se mișcă în planuri paralele. La rulare, unul sau mai multe puncte ale corpului atinge suprafața de-a lungul căreia se rotește corpul și în momentul contactului sunt imobile. Aceasta înseamnă că corpul are o axă de rotație instantanee care trece prin aceste puncte și se află în planul de-a lungul căruia corpul se rotește. În orice moment, mișcarea corpului poate fi privită ca o rotație în raport cu o astfel de axă instantanee. Rularea unui corp poate fi considerată ca suma a două mișcări: mișcarea de rotație în jurul unei axe care trece prin centrul de inerție al corpului și translațională cu viteza liniară a centrului de inerție. Energia cinetică a corpului de rulare constă din două părți:
Acolo υ0 - viteza de mișcare de translație a centrului de masă, I0 - momentul de inerție față de o axă care trece prin centrul de masă al corpului perpendicular pe planurile mișcării punctelor sale.
Energia cinetică este energia mișcării, este numeric egală cu munca pe care corpul o poate face până când se oprește. Când corpul se deplasează de la punctul 1 la punctul 2, forța forței exterioare pe această cale A12 este egală cu schimbarea energiei sale cinetice:
Pentru o schimbare elementară a stării
Energie potențială
Există forțe a căror activitate nu depinde de forma traiectoriei de conectare forței inițiale și finale tela.Takie poziții numite conservatoare sau potențial. Să explicăm acest lucru în Fig. 13. Dacă corpul se deplasează de la punctul 1 la punctul 2 de-a lungul căii 1a2, forța va executa lucrarea A1a2; Când se deplasează de-a lungul traiectoriei 1b2, lucrarea este egală cu A1b2. Prin definirea unei forțe conservatoare, A1a2 = A1b2. Forța de forță de-a lungul căii închise Ao (de exemplu, 1a2b1) este zero. Într-adevăr, Ao = A1A2 + = A2b1 A1a2- A1b2 = 0. De notat că, în direcția schimbării este inversată (vezi. Fig. 11), unghiul dintre vectorul forței și deplasarea este convertită în acute bont, cu cosinusului lor sunt diferite doar în semn. Aceasta înseamnă că dacă mișcarea forței într-o direcție este pozitivă, atunci în direcția opusă este negativă. Din aceasta urmează o altă proprietate a forței conservatoare - dispariția muncii pe orice traiectorie închisă.
Să arătăm că dintre cele trei forțe - gravitatea, elasticitatea și fricțiunea, primele două sunt conservatoare.
Lăsați corpul să acționeze gravitational, iar corpul se deplasează de la punctul 1 la punctul 2 (Fig.14). Vectorul gravitației m

Un rezultat similar este dat de forța elastică F = -kx:
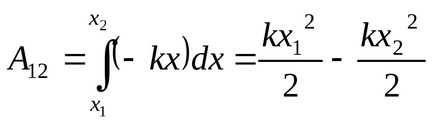
Forța de frecare nu este conservatoare. Într-adevăr, pentru orice direcție de mișcare această forță este îndreptată împotriva mișcării, lucrarea ei asupra oricărei deplasări elementare este negativă, prin urmare, lucrul pe o cale închisă nu este zero.
Lucrarea unei forțe conservatoare este egală cu o scădere a unei cantități care este o funcție a stării corpului și măsurată în SI în jouli. Această funcție este denumită energia potențială En. diferența dintre valorile sale în starea inițială -1 și în starea finală a celor două stări este egală cu forța forței atunci când corpul se deplasează de-a lungul oricărei traiectorii care leagă cele două poziții:
Cu o schimbare elementară (infinitezimală) în starea corpului
Se pare că am obținut deja formule pentru potențiala energie. Reamintim că energia potențială este energia interacțiunii, care depinde de poziția reciprocă a corpurilor. Energia potențială a corpului în câmpul gravitațional al pământului depinde de înălțimea lui h deasupra nivelului orizontal luat ca zero și se exprimă prin formula:
Pentru deformarea elastică, pentru un nivel zero al energiei potențiale, este natural să se ia o stare nedeformată, atunci formula pentru energia potențială a unui corp deformat elastic are forma: