Studiind fenomenele naturii, rezolvând probleme tehnice, întâlnim procese periodice care pot fi descrise prin funcții de un fel special.
O funcție y = f (x) cu domeniul D se spune că este periodică dacă există cel puțin un număr T> 0, astfel încât următoarele două condiții să fie valabile:
1) punctele x + T, x - T aparțin domeniului D pentru fiecare x ∈ D;
2) pentru fiecare relație x în D
f (x) = f (x + T) = f (x-T).
Numărul T este numit perioada funcției f (x). Cu alte cuvinte, o funcție periodică este o funcție a cărei valori se repetă după un anumit interval. De exemplu, funcția y = sin x este periodică (Figura 1) cu o perioadă de 2π.
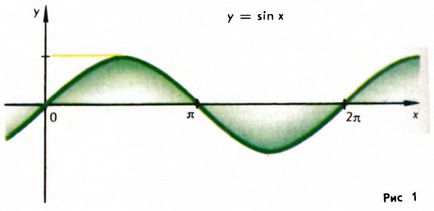
Rețineți că dacă numărul T este perioada funcției f (x), atunci numărul 2T va fi și perioada sa, cum ar fi 3T și 4T etc., adică funcția periodică are infinit mai multe perioade diferite. Dacă între ei există cel puțin (nu egal cu zero), atunci toate celelalte perioade ale funcției sunt multiplii ai acestui număr. Observăm că nu fiecare funcție periodică are o perioadă atât de mică, pozitivă; de exemplu, funcția f (x) = 1 nu are o astfel de perioadă. De asemenea, este important să rețineți faptul că, de exemplu, suma a două funcții periodice care au aceeași perioadă mai mică pozitivă T0. nu are neapărat aceeași perioadă pozitivă. Astfel, suma funcțiilor f (x) = sin x și g (x) = -s x nu are deloc cea mai mică perioadă pozitivă și suma funcțiilor f (x) = sin x + sin 2x și g (x) cele mai scurte perioade fiind de 2π, are cea mai mică perioadă pozitivă egală cu π.
Dacă raportul dintre două funcții f (x) și g (x) este un număr rațional, atunci suma produsului acestor funcții sunt, de asemenea, funcții periodice. Dacă raportul dintre perioadele de pretutindeni definite și funcții continue f și g este un număr irațional, atunci funcția f + g și fg vor fi deja funcții neperiodice. De exemplu, funcțiile cos x • • x păcat și √2 cosj √2 • sin x x + sunt nonperiodic, deși funcția sin x și cos x periodice cu perioada 2π, păcatul funcția √2 • x și cos √2 • x periodic cu o perioadă de √2 • π.
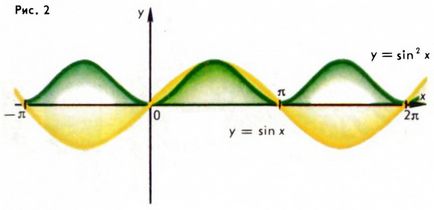
Rețineți că dacă f (x) este o funcție periodică cu perioada T, atunci funcția complexă (dacă, desigur, are sens) F (f (x)) este, de asemenea, o funcție periodică, iar numărul T va servi ca perioadă. De exemplu, funcțiile y = sin 2 x, y = √ (cos x) (figura 2.3) sunt funcții periodice (aici: F1 (z) = z2 și F2 (z) = √z). Cu toate acestea, nu trebuie să se presupună că, dacă funcția f (x) are cea mai mică perioadă pozitivă T0. atunci funcția F (f (x)) va avea aceeași perioadă minimă pozitivă; de exemplu, funcția y = sin 2 x are cea mai mică perioadă pozitivă, de 2 ori mai mică decât funcția f (x) = sin x (fig.2).
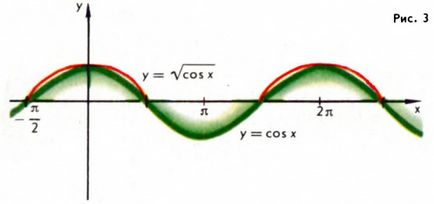
Este ușor de a arăta că, dacă funcția f este periodică cu perioada T, este definită și diferențiabilă la fiecare punct al liniei reale, funcția f „(x) (derivat) este de asemenea o funcție periodică cu perioada T, însă funcția primitivă F (x) (a se vedea. Integral calcul) pentru f (x) va fi o funcție periodică numai în cazul în care