Mecanica pentru descrierea mișcării corpurilor, în funcție de condițiile anumitor sarcini, utilizează diferite modele fizice. Cel mai simplu model este un punct material - un corp care are o masă a cărei dimensiuni în această problemă pot fi neglijate. Conceptul de punct material este abstract, însă introducerea acestuia facilitează rezolvarea problemelor practice. De exemplu, atunci când studiază mișcarea planetelor în orbite în jurul Soarelui, le putem lua pentru puncte materiale.
Un corp macroscopic arbitrar sau un sistem de corpuri poate fi împărțit mental în mici părți interacțioase, fiecare dintre ele fiind tratată ca punct material. Apoi, studiul mișcării unui sistem arbitrar de corpuri se reduce la studierea sistemului de puncte materiale. În mecanică, mișcarea unui singur punct material este studiată mai întâi și apoi continuă studiul mișcării unui sistem de puncte materiale.
Sub influența corpurilor unii pe alții, organismele se pot deforma, adică își pot schimba forma și dimensiunea. Prin urmare, în mecanică se introduce un alt model - un corp absolut rigid. Un corp absolut rigid este un corp care în nici un caz nu se poate deforma și în orice condiții distanța dintre două puncte (sau mai precis între două particule) ale acestui corp rămâne constantă.
Mișcarea corpurilor are loc în spațiu și timp. Prin urmare, pentru a descrie mișcarea unui punct material, este necesar să se știe în ce spații de spațiu acest punct a fost localizat și în ce moment a trecut această poziție. În sistemul SI, timpul este măsurat în secunde [t] = c.
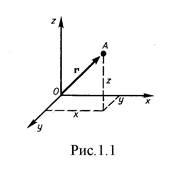
Poziția punctului material este determinată în raport cu orice alt organism ales arbitrar, numit organismul de referință. Cu acesta este un sistem de referință - totalitatea sistemului de coordonate și orele asociate corpului de referință. În sistemul de coordonate cartezian folosit cel mai adesea, poziția punctului A la un moment dat cu privire la acest sistem este caracterizată prin trei coordonate x, y și z sau un vector de rază. trase de la originea sistemului de coordonate la punctul dat (figura 1.1).
Atunci când punctul material se mișcă, coordonatele se schimbă odată cu timpul. În cazul general, mișcarea sa este determinată de ecuațiile scalare
echivalentă cu ecuația vectorului
Ecuațiile (1.1) (respectiv, (1.2)) sunt numite ecuațiile cinematice de mișcare ale unui punct material.
Numărul de coordonate independente care determină complet poziția unui punct în spațiu se numește numărul de grade de libertate. Dacă punctul material se mișcă liber în spațiu, atunci, așa cum am menționat deja, are trei grade de libertate (coordonatele x, y și z); dacă se mișcă de-a lungul unei anumite suprafețe, atunci - cu două grade de libertate, dacă de-a lungul unei anumite linii, atunci - de un grad de libertate.
Eliminând t în ecuațiile (1.1) și (1.2), obținem ecuația traiectoriei mișcării punctului material. Traiectoria mișcării unui punct material este o linie descrisă în acest punct în spațiu. În funcție de forma traiectoriei, mișcarea poate fi rectilinie
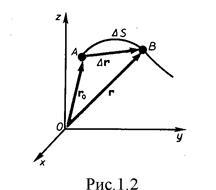
Să considerăm mișcarea unui punct material de-a lungul unei traiectorii arbitrare (figura 1.2). Începem să numărăm momentul din momentul în care punctul era în poziția A. Lungimea secțiunii traiectoriei AB. trecut printr-un punct material din momentul originii timpului, se numește lungimea căii Și este o funcție scalară a timpului în # 916; s = # 916; s (t). Dimensiunea traseului este în metri (m). Vector. trase din poziția inițială a punctului de mișcare în poziția sa la un moment dat (creșterea incrementului vectorului de rază al punctului din intervalul de timp considerat) se numește deplasare.
Cu mișcare rectilinie, vectorul de deplasare coincide cu secțiunea corespunzătoare a traiectoriei și modulul de deplasare este egal cu traiectoria traversată # 916; s.
Pentru a caracteriza mișcarea unui punct material, introducem o cantitate vectorială, viteza care determină atât viteza mișcării cât și direcția acesteia la o anumită clipă de timp.
Fie punctul material să se deplaseze de-a lungul oricărei traiectorii curbilinii, astfel încât la momentul t să corespundă unui vector de rază (Figura 1.3). Într-o perioadă scurtă de timp T Punctul va trece calea Și vor primi o deplasare elementară (infinit de mică).
Vectorul vitezei medii este raportul incrementului radius-vector al punctului cu intervalul de timp # T16:
Direcția vectorului de viteză medie coincide cu direcția. Cu o reducere nelimitată, viteza medie tinde spre valoarea limită, care se numește viteza instantanee:
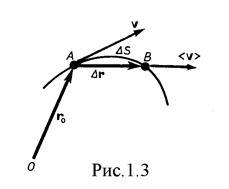
Viteza instantanee. Astfel, există o cantitate vectorală egală cu prima derivată a vectorului de rază al punctului mobil în timp. Dimensiunea vitezei în CM - metru pe secundă (m / s). Deoarece secantul coincide cu tangenta in limita, vectorul de viteza este tangent la traiectoria in directia miscarii (Figura 1.3). Pe măsură ce calea scade Se va aborda din ce în ce mai mult. astfel încât modulul de viteză instantanee
Cu mișcare neuniformă, modulul de viteză instantanee se schimbă cu timpul. În acest caz, utilizați valoarea scalară - rata medie de mișcare neuniformă:
Din fig. 1.3 rezultă că, din moment ce # 916; s>. și numai în cazul mișcării rectilinii
Dacă expresia ds = Dt (vezi formula (1.4)) se integrează în timp în intervalul de la t la t + , Atunci găsim lungimea căii traversată de punctul în timp # T16:
În cazul mișcării uniforme, valoarea numerică a vitezei instantanee este constantă; atunci expresia (1.5) ia forma
Lungimea căii traversate de punct pentru un interval de timp de la t1 la t2 este dată de integrale