
Acasă | Despre noi | feedback-ul
Dintre mii de oameni care au fost amuzați în copilărie cu un vârf, nu mulți pot răspunde corect la această întrebare. Cum, de fapt, să explicăm faptul că vârful de filare, așezat vertical sau chiar oblic, nu se răstoarnă, contrar așteptărilor? Ce forță îl păstrează într-o situație atât de aparent instabilă? Nu îl afectează gravitatea?
Aici există o interacțiune foarte interesantă a forțelor. Teoria topului nu este simplă și nu vom intra în ea. Vom sublinia doar motivul principal, din cauza căruia nu se încadrează vârful rotativ.
În Fig. 26 prezintă un giroscop rotativ în direcția săgeților. Notați partea A a jantei sale și partea B opusă acesteia. Partea A încearcă să se mute de la tine, partea B - pentru tine. Acum, vedeți ce mișcare primesc aceste părți atunci când înclinați partea superioară a vârfului spre dumneavoastră. Cu această mișcare faceți partea A în sus, partea B - în jos; ambele părți primesc o lovitură la un unghi drept față de propria mișcare. Dar, ca și cu rotirea rapidă a o viteză maximă periferică a părților discului este foarte mare, a fost ați raportat o ușoară viteză, se adaugă până la un mare punct de viteză circulară, dă o rezultantă, foarte aproape de această circulară - și mișcarea de sus este aproape neschimbat. Prin urmare, este clar de ce partea de sus pare să reziste încercării de ao răsturna. Cu cât este mai masivă din partea de sus și mai repede se învârte, cu atât mai mult cu încăpățânare el rezista bascularea.
Figura 26. De ce nu cădea partea de sus?
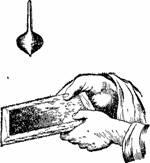
Figura 27. Suprafața rotativă, aruncată, păstrează direcția inițială a axei sale.
Esența acestei explicații este legată direct de legea inerției. Fiecare particulă din partea superioară se mișcă de-a lungul unui cerc într-un plan perpendicular pe axa de rotație. Conform legii inerției, particula în orice moment tinde să treacă de la cerc la o linie dreaptă tangentă la cerc. Dar fiecare tangent este în același plan ca și cercul în sine; astfel încât fiecare particulă tinde să se miște astfel încât să rămână în planul perpendicular pe axa de rotație. Rezultă că toate planurile din partea superioară, perpendiculară pe axa de rotație, tind să-și mențină poziția în spațiu și, prin urmare, perpendicularul comun pe ele, adică axa de rotație în sine, tinde, de asemenea, să-și mențină direcția.
Nu vom lua în considerare toate mișcările de sus, care apar atunci când o forță străină acționează asupra ei. Acest lucru ar necesita explicații prea detaliate, care, probabil, par plictisitoare. Voiam doar să explic motivul dorinței fiecărui corp rotativ de a menține neschimbată direcția axei de rotație.
Această proprietate este utilizată pe scară largă de tehnologia modernă. Diferite instrumente giroscopice (bazate pe cea mai bună calitate) - busole, stabilizatoare etc. - sunt instalate pe nave și aeronave [11].
Aceasta este o utilizare utilă a jucăriilor simple, aparent.
Multe trucuri uimitoare ale unui program divers de jongleri se bazează, de asemenea, pe proprietatea corpurilor rotative pentru a menține direcția axei de rotație. Permiteți-mi să citez un extras din cartea fascinantă a fizicianului englez prof. John Perry "Spinning top".
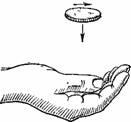
Figura 28. Cum funcționează moneda zburată cu rotație.
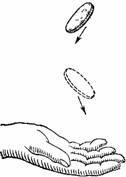
Figura 29. O monedă aruncată fără rotire, cade într-o poziție aleatorie.
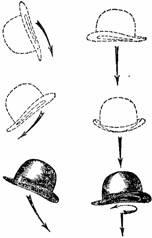
Figura 30. O pălărie aruncată este mai ușor de prins dacă a fost anunțată rotația în jurul axei.
Într-o zi am arătat câteva din experiențele mele pentru public, a băut cafea și tutun kurivshey în sala de concert magnific din interior „Victoria“ din Londra. Am încercat să intereseze studenții mei am putut, și a spus că inelul plat este necesar să se informeze rotația, în cazul în care acesta este dispus să renunțe, astfel încât să puteți specifica în avans, în cazul în care acesta va cădea; doar vin, în cazul în care doresc pe cineva # 8209; unii arunca pălăria, astfel încât el ar putea prinde acest stick de lucru. Este întotdeauna posibil să se bazeze pe rezistență, care are un corp de rotație, atunci când schimbă direcția axei sale. În continuare, am explicat studenților mei că, butoi neted lustruit al unui pistol, nu vă puteți baza pe acuratețea vederea; Prin urmare, acum face filetat botul, t. e. tăietură pe interiorul jgheabului arme baril în spirală, în care proiecțiile se încadrează nucleu sau coajă, astfel încât acesta din urmă ar trebui să primească o mișcare de rotație atunci când forța exploziei prafului de pușcă face deplasa prin arma de canal. Datorită acestui fapt, proiectilul părăsește arma cu o mișcare precisă de rotație.
A fost tot ce am putut face la momentul acestui curs, din moment ce nu am dexteritate în aruncarea pălării sau discuri. Dar, după ce am terminat conferința mea pe scenă au fost două jongler - și nu am putut dori o mai bună ilustrare a legilor menționate mai sus, mai degrabă decât cea care a dat fiecare individ se concentreze, așa cum este arătat de acești doi artiști. Ei au aruncat reciproc rotative pălării, împachetări, farfurii, umbrele ... Unul dintre jongleri aruncat în aer o varietate de cuțite, le prinde din nou și din nou, au aruncat cu mare precizie în sus; publicul meu, doar pentru a asculta explicația acestor fenomene, tresăltau cu plăcere; ea a observat rotație, care se raportează la fiecare cuțit jongler, lasandu-l sa plece, ca, probabil, el ar putea ști în care poziția cuțitul din nou veni înapoi la el. Am fost apoi uimit că aproape fără excepție, trucuri jonglerie prezentate în seara, este o ilustrare a principiului de mai sus. "