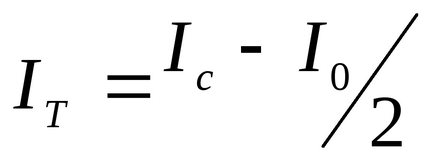Shestakov IG (complot 513)
Obiectiv: Determinarea momentelor de inerție a substanțelor solide.
Aparatură și materiale: suspensii Trifilyarny, iluminator, scara translucide, mai multe corp geometric diferit de măsurare, cu o precizie de cronometru 0.2S, caliper.
Trifilyarny suspensie este o platformă circulară suspendată pe trei filamente dispuse simetric înscrise la marginile platformei. Deasupra acestor fire, de asemenea, atașate simetric pe raza discului mai mic decât diametrul platformei. Platforma poate efectua oscilații de torsiune în jurul unei axe verticale perpendiculare pe planul său și care trece prin centrul său. Aceste oscilații pentru o perioadă scurtă de timp și fără alte oscilații armonice își poate asuma. Perioada de oscilații depinde de momentul inerției platformei. Să găsim această dependență. Lăsați unghiul maxim de rotație al platformei să fie 0. Trecând la unghiul 0. platforma se ridică simultan la înălțimea h, dobândind potențialul de energie mgdh. La returnarea platforma în poziția de echilibru mgh energie potențială este transformată în energie cinetică a mișcării de rotație J0 2/2.
În conformitate cu legea conservării energiei, putem scrie:
Fie variază în conformitate cu legea sinusului:
Când platforma trece poziția de echilibru, viteza sa unghiulară atinge valoarea maximă. care pot fi găsite din relația (2).
Deoarece unghiul 0 este mic, putem aproxima h1 + h2 = 2l și apoi
Înlocuind aceste valori în (1), obținem:
Folosind (1), (3), (4), găsim:
J = mgRrT2 / 4p 2 l (5)
Dacă un corp este plasat pe o platformă, momentul inerției sistemului va fi diferit. Măsurarea momentului de inerție J0 când platforma neîncărcată și momentul J inerție al sistemului cu corpul, se poate determina momentul de inerție a corpului JT.
Cantitățile l, R, r și masa platformei m0 sunt date ca constante ale dispozitivului. Prin urmare, măsurătorile se reduc numai la determinarea masei corpului și a perioadei de oscilații.
Oscilația este excitată prin rotirea discului superior.
Pentru a crește precizia măsurătorilor de timp, se utilizează o scală, un iluminator și o oglindă, montate pe o platformă.
Calculul teoretic al numărului de oscilații care trebuie luate pentru a determina perioada, astfel încât calculul erorii relative pentru valoarea numerică a momentului de inerție a fost făcut utilizând următoarea formulă:
Calculul erorii pentru valoarea numerică a momentului de inerție obținut experimental și calculat prin formula (6) a fost făcut utilizând următoarea formulă
Pentru ca eroarea să fie minimă la calcularea momentului de inerție, Summand-ul trebuie să fie mult mai mic decât toate celelalte (în
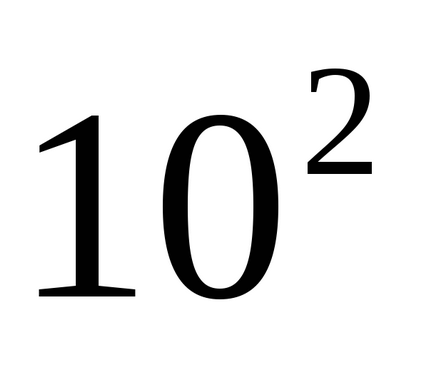
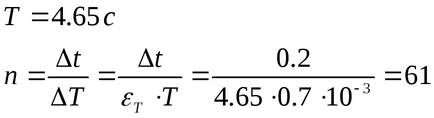
Datorită faptului că fluctuațiile în acest caz sunt amortizate, iar formula (5) este valabilă numai pentru vibrațiile armonice, numărul de oscilații egal cu
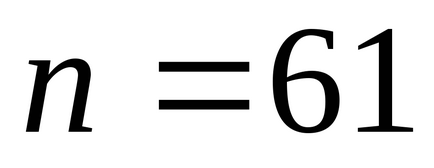
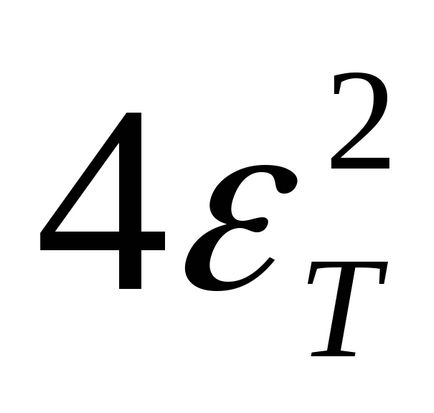
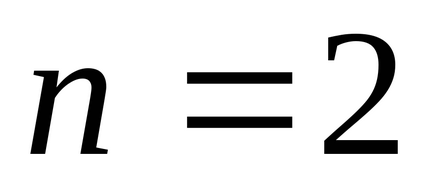
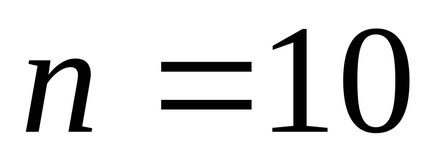
Determinarea momentului inerției unei platforme goale. Parametrii suspensiei trifilare se compun în toate experimentele efectuate, numărul de oscilații ale platformei a fost n = 10. Rezultatele obținute experimental sunt prezentate mai jos.
După înlocuirea valorilor numerice în formulele (5) și (6), s-a obținut valoarea experimentală a momentului de inerție al inelului:
Valoarea teoretică a momentului de inerție a fost calculată prin următoarea formulă:
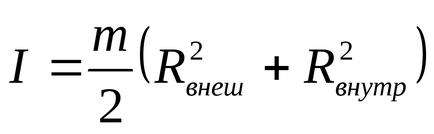
După înlocuirea valorilor numerice din această formulă, s-a obținut următorul rezultat:
Determinarea momentului de inerție a emisferei este experimental și teoretic. Dimensiunile fizice ale emisferei sunt Valorile numerice ale perioadei de oscilație sunt prezentate mai jos:
După înlocuirea valorilor numerice în formulele (5) și (6), s-a obținut valoarea experimentală a momentului de inerție al inelului:
Valoarea teoretică a momentului de inerție a fost calculată prin următoarea formulă:
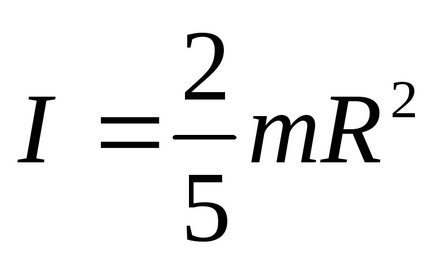
După înlocuirea valorilor numerice din această formulă, s-a obținut următorul rezultat:
5. Verificarea teoremei lui Huygens-Steiner. În acest experiment, a fost folosit un cilindru tăiat de-a lungul înălțimii cu două semi-cilindri identici. Dimensiunile fizice ale acestui corp sunt,
Valoarea experimentală a momentului de inerție al sistemului a fost calculată prin formula (5), iar momentul inerției corpului a fost calculat prin următoarea formulă