Revolving pendul - un dispozitiv pentru determinarea experimentală a accelerării padeniyag. Este un pendul fizic.
pendul fizică este orice solid. care, sub forța gravitației poate efectua oscilații libere cu privire la un punct fix. Cel mai simplu descrise printr-o mișcare de pendul plan în jurul unei axe fixe. Cazul De fapt, în cazul în care pendulul efectuează câteva zeci de vibrații, fără atenuare semnificativă. frecare forței de cuplu într-o primă aproximare, poate fi neglijată.
Aplicarea pendul de lucru pentru măsurarea accelerației gravitaționale bazată pe proprietatea centrului swing conjugare și punctul de suspendare. Această proprietate constă în faptul că cel puțin pendulul fizic este posibil să se găsească două puncte situate pe laturile opuse ale centrului de masă. că suspendarea secvențială pendulul într-unul și celălalt dintre ele în timpul oscilației pendulului rămâne neschimbat. Distanța dintre aceste puncte determină așa-numitul lungimea redusă a unui pendul fizic.
Realizată sub formă, de exemplu, placă solidă (1), cu două cuțite cu trei tăișuri, dintre care unul este fix, iar celălalt se pot deplasa de-a lungul fantelor de pe placa. Muchiile ascuțite O1 și O2 cuțite. alternativ plasat pe un suport fix, servesc ca axe de leagăn a pendulului de lucru. Cuțitul mobil este deplasat în sus sau în jos până când perioadele de oscilație pendul care gravitează în jurul fiecărei axe (măsurată prin cronometru) nu coincid. O12 = distanța L dintre axele se măsoară cu ajutorul unei plăci de aplicat pe scara Vernier. Apoi, de proprietățile fizice ale pendulului pentru O1 O2 va swing centrul și vice-versa, iar perioada oborotnogo mici oscilații ale pendulului va astfel egal cu
.
Și definind o valoare J din experiență, poate fi calculată prin formula, g. Revolving pendul pentru a determina amploarea g cu un grad semnificativ mai mare de precizie decât pendulului matematic.
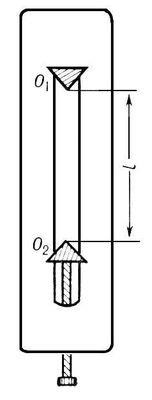
Revolving pendul - un dispozitiv pentru determinarea experimentală a accelerării padeniyag.
pendule curente utilizate în determinarea accelerației gravitaționale, în funcție de cerințele care le sunt prezentate au forme foarte diferite. Ele constau, de obicei, dintr-o tijă metalică, care se poate deplasa de-a lungul, și fixat într-o anumită poziție a încărcăturilor grele și ușoare și lagărul prismei. Diferite combinații de sarcini și pozițiile lor asupra benzii în raport cu marginile de susținere oferă diferite tipuri de pendule circulant (Fig.1).
Design standard de lucru cu pendul

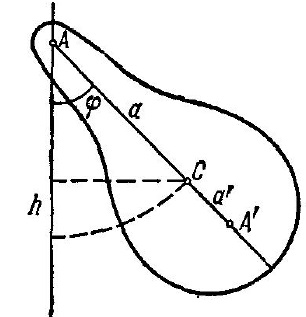
pendul fizic numit corp solid, care poate pivota în jurul unei axe fixe orizontală. Un punct de intersecție dintre planul său vertical care trece prin centrul maselor pendul, numit punctul de suspensie al pendulului (Fig. 1). poziția corpului, în orice moment dat poate fi caracterizată prin unghiul de deviere de la φ poziția sa de echilibru. Unghiul cp joacă rolul q coordonate generalizate. Energia cinetică a pendulului fizic oscilant este dată de
unde I - momentul de inerție al pendulului în raport cu axa A. Energia potențială este Epot = mgh, unde h - înălțimea centrului de elevație C în masă deasupra poziției sale cea mai joasă. Notăm distanța dintre centrul de masă C și punctul de suspensie A. Apoi
În cazul unor fluctuații mici sinusul unghiului φ / 2 poate fi înlocuită cu aproximativ unghiul. În această apropiere,
Astfel, pentru oscilații mici de energie potențială și cinetică la forma
,
în care α = mga, β = I. Rezultă că vibrațiile mici vor fi un pendul fizic cu frecvența unghiulară aproximativ armonică
Teorema Huygens-Steiner (numit după matematicianul Yakova Shteynera și matematician olandez, fizician și astronom Hristiana Gyuygensa): momentul corpul de inerție I față de o axă arbitrară este suma momentului de inerție al corpului Ic în jurul unei axe care trece prin centrul de masă al corpului paralelă cu axa considerată și produsul m greutate corporală la pătrat R distanța dintre axele:
unde m - masa corpului și R - distanța dintre axele.
Este nevoie de frame-uri inline de sprijin.