Rândurile sunt numite de alocare număr de serie, care caracterizează structura agregatului pe unele motive. O distribuție număr poate fi obținut ca urmare a unor grupuri structurale. Mai multe distribuție formate prin variabile (interval de variație) pot fi discrete (atribut are un număr limitat de valori posibile, de exemplu 2,3,4,5) sau intervalul (valori caracteristice exprimate prin numere reale, sau numărul de posibile valori atribut este suficient de mare).
Caracteristicile seriei sunt:
xi - varianta (posibila valoare caracteristica numerică separată)
ni - frecvența (numărul de grupuri separate);
n - numărul total de elemente împreună;
qi - frecvența relativă (proporția grupurilor individuale în totalitate).
seria variațională este făcută într-un tabel în care prima coloană indică variante (intervale) de valori de funcții, iar în următoarele - frecvența și frecvența relativă.
Un număr de distribuție în ansamblu caracterizează structura agregatului pentru o anumită trăsătură. Cu toate acestea, pot fi utilizate și seriile cumulative, și anume rânduri de frecvență cumulativă (frecvențe relative).
frecvență cumulativă (frecvența relativă) - este numărul (fracțiunea) din elemente ale setului în care valorile caracteristică nu depășesc acest lucru.
F (x) - frecvență cumulativă pentru o anumită valoare a lui x;
G (x) - frecvența relativă cumulativă pentru o valoare x dată.
Aceste caracteristici au următoarele proprietăți:
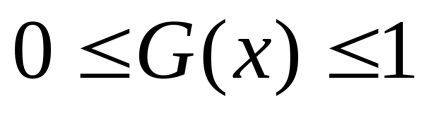
Luați în considerare intervalul cu numărul i. [xi
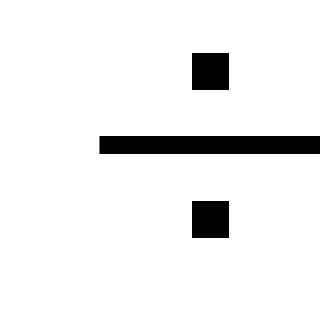
frecvență Acumulate la sfârșitul intervalului i-lea definit prin formula
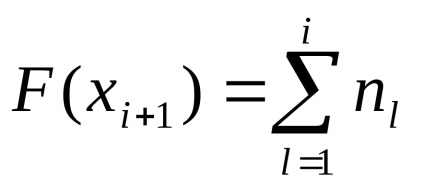
Numărul de variație poate fi reprezentat ca un grafic.
Imaginea unei serii discrete a unui poligon. Când este pe baza exemplelor de realizare abscisa (xi), iar ordonata - frecventa relativa sau frecventa - fi. Apoi, punctul cu coordonatele (xi; fi) segmente de linie conectate succesiv.
Imaginea seriei intervalului este histograma. În construcția sa pe abscisă intervalele ale seriei. Deasupra abscisa dreptunghi construit a cărui bază este intervalul și înălțimea - frecvența sau frecvența relativă.
Numărul imaginii acumulat de frecvențe este cumulează. frecvență cumulativă reprezentate pe intervalele axa y pentru granițele și sunt conectate prin segmente de linie.
Exemplul 1. Distribuția apartamentelor cu privire la numărul de locuitori este prezentată în tabelul de la domiciliu. Construirea unui poligon și cumulează.
Numărul de persoane care trăiesc în apartament
Găsim mediana. În acest caz,
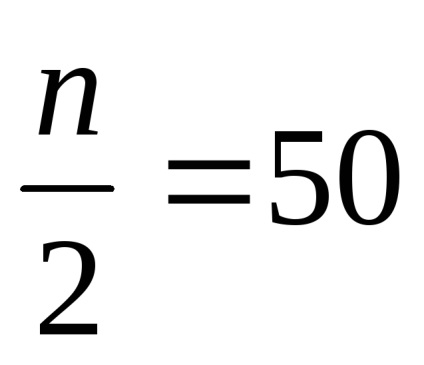
Vom găsi de moda de la aceste date. Moda este în același interval ca și frecvența maximă (25), sunt în acest interval.
.
.
.
abaterea standard
Pe baza grupurilor structurale de al doilea indicator obținut în sarcină 1 și cumulând histograma.
Calculat din datele grupate:
varianței și abaterea standard;
Statisticile absolute și relative. Calcularea o valoare medie a indicatorilor relativi.
În conformitate cu cifrele absolute în statisticile pentru a înțelege anchetele statistice de referință (volumul de producție, numărul de persoane și așa mai departe. D.). Ele pot fi, fie un cuplu (la un moment dat) și un interval (pentru o anumită perioadă). Orice valoare absolută (indice) are unitate inerentă de măsurare (bucăți, kilograme, metri și altele asemenea. D.). De multe ori în parametrii de cost (în ruble), este utilizat ca indicatori absoluți.
În conformitate cu indicatorii relativi în statistici pentru a înțelege cifrele, ce caracterizează raportul dintre doi indicatori absolute (PIB pe cap de locuitor, productivitatea muncii, costurile de producție și așa mai departe. D.).
Distinge valori relative structură, coordonare, dinamică, intensitate și de comparație.
Valorile relative reprezintă procentajul din structura fiecărui grup în populația totală. Ele se obțin prin împărțirea numărului fiecărui grup de mărimea întregii populații.
Valorile relative obținute coordonate ca raportul dintre părțile unui set. De exemplu, poate fi raportul dintre bărbați la femei.
Mărimile relative ale comparației este obținută prin compararea celor două figuri de același nume, aparținând diferitelor agregate. De exemplu, atunci când se compară valoarea activelor fixe două regiuni diferite.
Magnitudinea relativă a intensității este obținută prin compararea semnelor de un set de sarcini opuse. De exemplu, rata fertilității este raportul dintre numărul de nașteri la numărul de locuitori, iar costul de producție este raportul dintre totalul cheltuielilor pentru producția de volum.
Pentru a calcula valorile medii ale valorilor relative ale diferitelor formule utilizate medii ponderate pe baza indicatorilor economici ai înțeles. Statisticile utilizate de diferite tipuri de medii.
Cel mai adesea următoarele valori medii se aplică:
Toate aceste valori medii pot fi calculate prin puterea medie formula generală
În cazul în care datele sunt grupate, apoi
Ultimele două formule permit obținerea de diferite tipuri de medii, cu diferite valori ale lui m (vezi. Tabelul).
Media aritmetică, o medie armonică, media geometrică și medie pătrată calculată pentru aceleași date de intrare sunt diferite unele de altele. Există întotdeauna următoarea relație:
Iată câteva exemple de utilizare a dependențelor medii ponderate.
Exemplul 1. Găsiți coeficientul mediu de performanță al planului pe ramura întreprinderilor.
Să - planul lea al întreprinderii j-;
- planul de execuție relativ index (în fracțiuni);
n - numărul de industrie.
Apoi, volumul real al producției va fi
Volumul de producție planificat pentru industrie
Mediana planului pentru sectorul
Acest indice este media ponderată valorile aritmetice cu greutăți planului de producție corespunzătoare -.
Exemplul 2. Găsiți viteza medie a vehiculului în cazul în care distanța parcursă S1, la o viteză v1. și apoi S2 distanța la o viteză v2. Pentru a găsi viteza medie este necesară pentru a împărți distanța totală S1 + S2 pe timpul total petrecut în acest fel. Timpul total călătorie va fi egală cu
Astfel, viteza medie va fi
În general, prezența n secțiuni cu viteză diferită
Se observă cu ușurință că viteza medie este o medie ponderată a vitezelor armonice pe secțiuni individuale, cu ponderi egale cu lungimea secțiunilor de cale.