Teoria Rezumat I
F
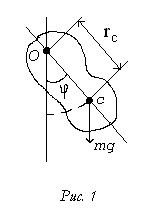
Notăm RC distanța de la axa de rotație la centrul de masă. Pendulum, poziția în afara bilanțului ar fi să oscileze. Poziția pendulului, poate fi caracterizată printr-un unghi de deviere (


Mișcarea corpului în raport cu ecuația momentelor axei fixe definite:
Momentul forțelor externe Mvnesh constă din momentul gravitate
iar cuplul de frecare. De multe ori, ca o aproximare brută, se crede că frecarea poate fi neglijată. Momentul de pendul impuls
unde J - momentul de inerție al pendulului în raport cu axa de rotație.
Ecuațiile Considerând (2) și (3) ecuația impulsului (1) poate fi rescrisă ca:
În această ecuație, o funcție necunoscută este o funcție a - unghiul pendulului de deflexie și a derivatelor sale de timp: viteza unghiulară și accelerație unghiulară. Ecuația (4) este valabilă pentru orice amplitudine a oscilației pendulului. Este mult mai simplu, în cazul unor oscilații mici ale pendulului atunci când unghiul de deviație de la poziția de echilibru este mic
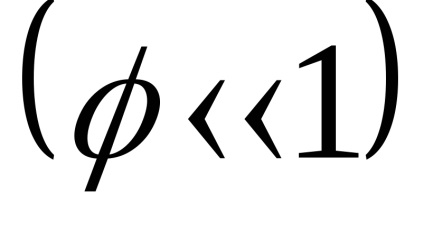
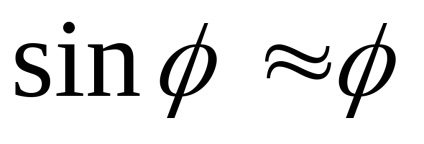
A doua ecuație diferențială comandă (5) are o soluție în forma:
în care A - amplitudinea de oscilație,
Vom arăta prin substituție directă că
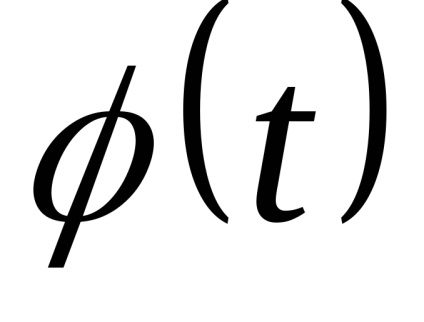
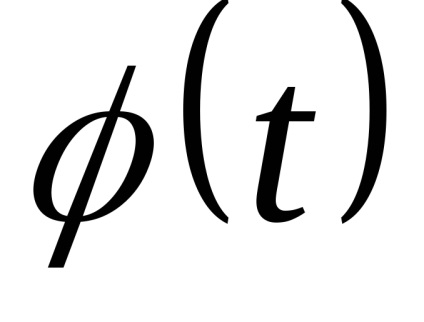
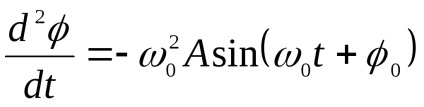
Înlocuim această expresie în (5)
Relația obținută este îndeplinită în orice moment, cu condiția ca:
Prin urmare, frecvența unghiulară a oscilației pendulului
Ecuația de mișcare (

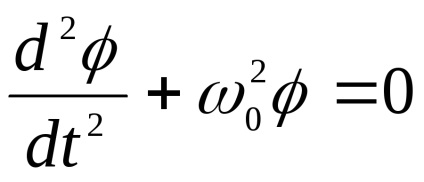
oh
Pendulul poate oscila într-un plan vertical, în repaus marginea inferioară a uneia dintre prismele de pe suprafața suport fix.
Ecuația (7) poate fi utilizată pentru determinarea accelerației de cădere liberă g. Acest lucru necesită izmeritT, J, rc.
Folosind un pendul de lucru (metoda pendulului de lucru) vă permite să stabiliți g, prin faptul că nu izmeryayaJ irc. Faptul că pe ambele părți ale centrului de masă al pendulului are o poziție de lucru a marginilor de susținere în care perioadele de oscilații ale pendulului coincide (a se vedea. Application).
Notăm RC1 IRS2 (RC1
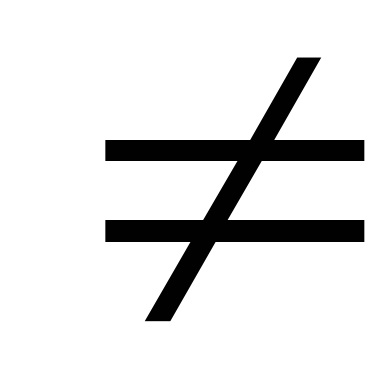
ecuația Dată (7)
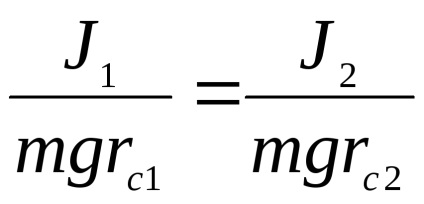
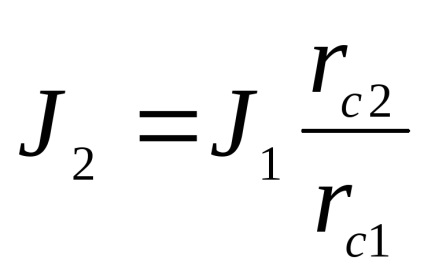
Prin teorema lui Steiner
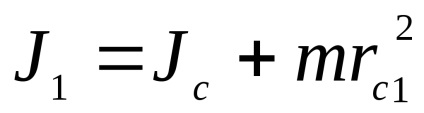
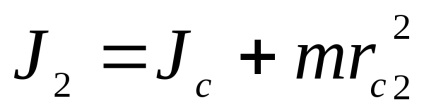
Din ultima ecuație ne putem exprima momentul de inerție al pendulului în raport cu centrul maselor oscilante
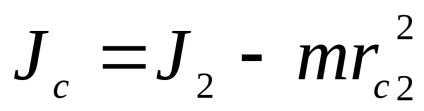
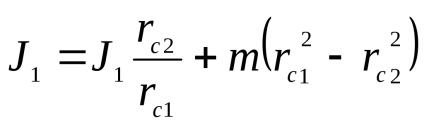
Definirea J1 și substituind această expresie în
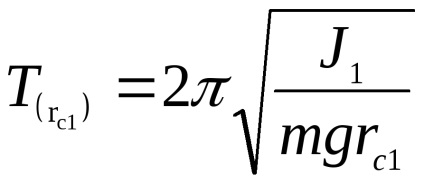
Exact aceeași formulă poate fi obținută pentru
În consecință, accelerarea cădere liberă poate fi determinată prin formula:
Pentru a găsi gdostatochno măsură numai două valori: distanța (RC1 + RC2) între coaste și prisme de susținere perioada de oscilație pendulului în polozheniirc1 și polozheniirc2 „inversat“. Acest lucru, chtorc1
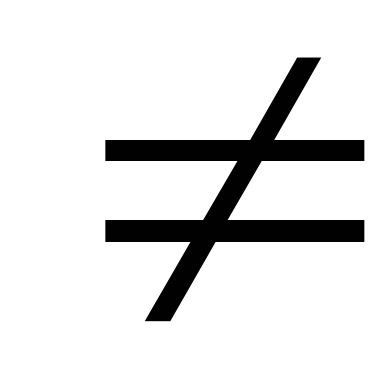
Sarcina rasstoyaniyrc1 1. Selectarea irc2. în care
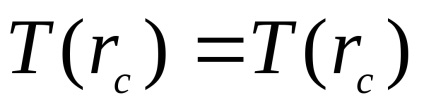
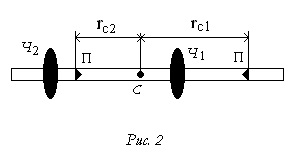
încărcături mobile este fixat pe tija în poziții asimetrice (Figura 2): o sarcină - la capătul tijei, celălalt - în apropierea centrului său.
determina cu aproximație poziția centrului de masă cu pendul. Una dintre prisme drepte consolidate la cel mai mare, distanța posibilă RC1 de la centrul de masă (aproape de capătul tijei). Al doilea - pe cealaltă parte a centrului de masă aproape la punctul C. în această perioadă situație determinată
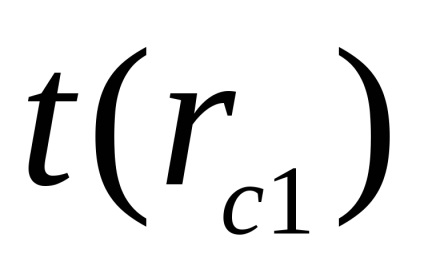
Apoi, fără a schimba poziția de marfă (pendul inversat), determina timpul
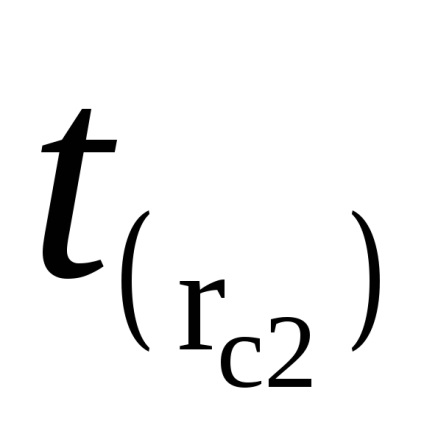
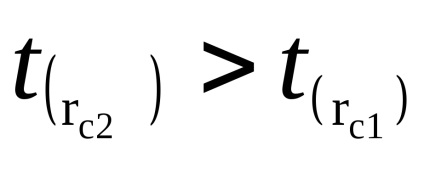
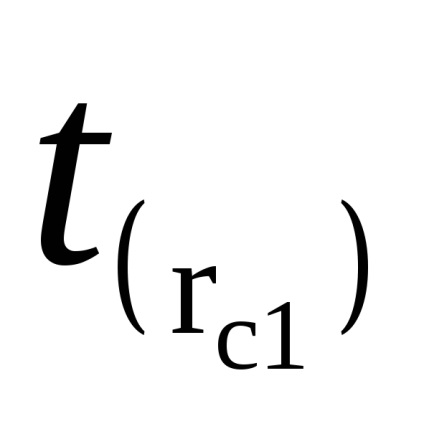
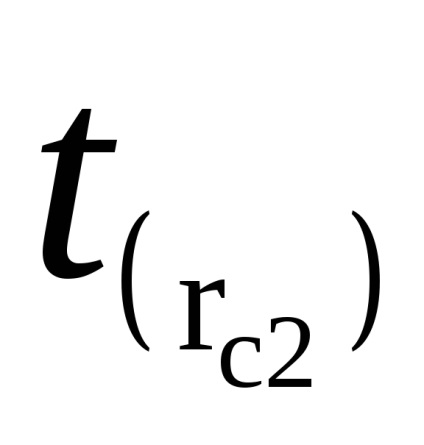
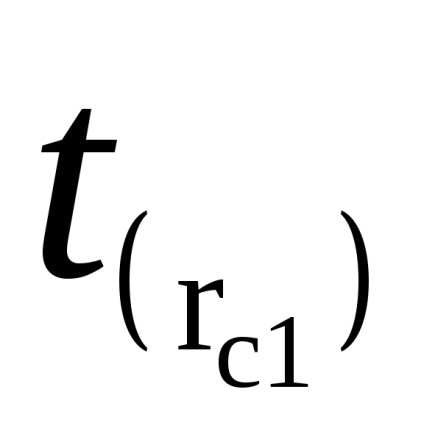
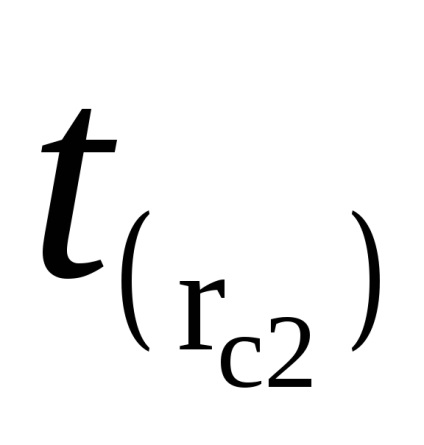
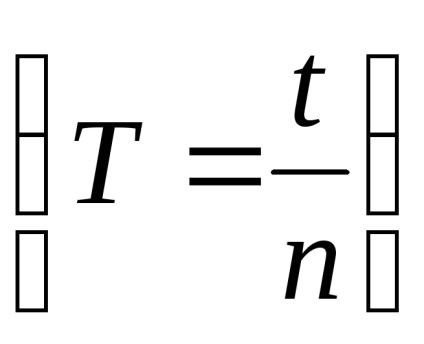
Sarcina 2. Determinarea accelerației gravitaționale.
Identificati timp de 50 de oscilații (de trei ori) t (RC1) și t (RC2). Completați în tabel.
Se măsoară distanța (RC1 + RC2).
Calculați accelerația gravitațională prin formula (9).
eroarea de măsurare instrument de înregistrare (cronometru și conducător).
Se calculează eroarea relativă metoda derivare și determină un interval de încredere
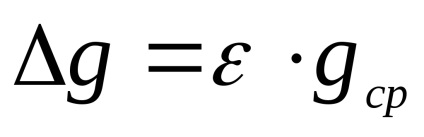
Sarcina 3. Determinarea poziției centrului de masă pendul.
Pendulul lungimea tijei 1,25m, massamst = 0,260 kg; greutate prismei este de 0,22 kg și 0,175 kg; linte greutate 0,930 kg și 1,44 kg.
Din aceste date și distanțele tuturor mărfurilor de la un capăt al tijei (măsura) definește valoarea teoretică a centrului de masă. Comparați-l cu centrul valorii poziției gravitate găsită experimental pe pendul, cu care calculul a fost realizat g.
Definiți cantitățile fizice: cuplu, moment de inerție, organisme impuls în raport cu axa; direcția lor?
Formulați ecuația de momente.
Ieșire perioadă formula de oscilație a unui pendul fizic.
Ce valoare se numește lungimea redusă a pendulului fizic?
Ceea ce se numește pendul negociabil? Avantajul său în determinarea g?
Formulele pentru determinarea gmetodom pendul rotativ.
Este posibil să se determine g, folosind teorema lui Steiner și cunoașterea momentului de inerție
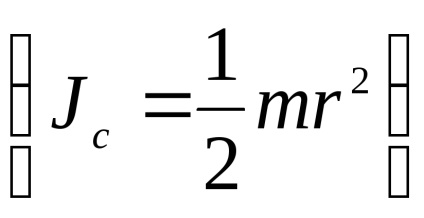
Determinate de eroarea absolută a perioadei de oscilație.
Oricare dintre acestea este în laborator determinată cu mai puțină precizie: T sau (RC1 + RC2)?
Are sens pentru a crește precizia de determinare a perioadelor complete meci de gdobivatsya? De ce?
Dovedește. Că atunci când perioadele de oscilatie pot fi considerate egale în termen de 10 -3 la?
Depind dacă perioadele de vibrație a pendulele fizice, lucru de greutatea lor?
Ia formula pentru determinarea

Cum de a identifica centrul de masă al pendulului experimental și teoretic de parametrii cunoscuți ai pendulului?
Sivukhin AV „Cursul general al fizicii“ v.1. Mecanică. M. 1976. pp. 166-170, 172-173, 209-213.
Arhanghelul MM „Cursul fizicii.“ Mecanică. M. 1975. pp. 297, 301-305, 315-316, 327-328.
Aleksandrov, NV Yashkin AY „Cursul de fizica generala.“ Mecanică. M. 1978. pp. 335-336.
Savelyev IV „Curs de Fizică“ v.1. Mecanică. Fizica moleculara. M. 1989. pp. 101-107.
Gershenzon EM NN Malov „Cursul de fizica generala.“ Mecanică. M. 1979. pp. 85-89.
Un avantaj al metodei de lucru a pendulului pentru determinarea accelerației de cădere liberă este că irc I0 nu sunt incluse în formula de calcul dlyag. Ne întoarcem acum la o discuție a acestei metode.
Conform teorema lui Huygens-Steiner, momentul de inerție al pendulului pendulează în jurul axei O
unde Ic - pendulul momentului de inerție față de o axă paralelă cu axa de balansare și care trece prin centrul de masă C a pendulului, rc - distanța dintre axele O și S.
Furnizarea (2) în (1) obținem
Vom discuta calitativ dependența perioadei de oscilație printr-o rc distanță pentru a se balanseze axa. La foarte malyhrc. punct de gravitate
M = sin -mgrc


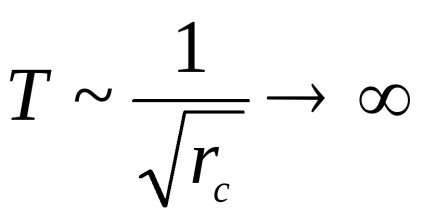
În limita opusă a rc foarte mari poate prenebrechIs comparativ CMR
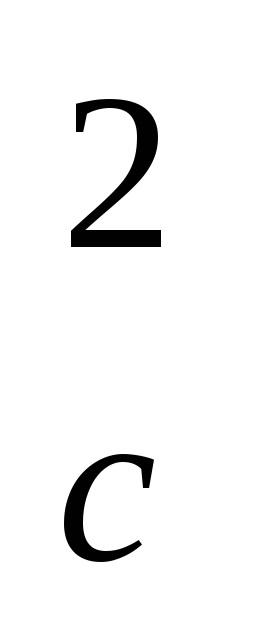
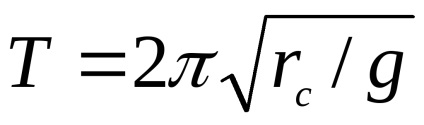
P

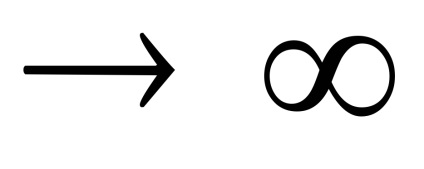
Valoarea rc = 0 corespunde centrului de masă al pendulului. În cazul în care pendulul este suspendat pe cealaltă parte a centrului de masă, așa cum reiese din formula (3), dependența T (rc) va fi exact la fel. Prin urmare, graficul T (RC) are două ramuri simetrice corespunzătoare punctului de suspensie pendul la stânga sau la dreapta centrului său de masă.
Graficul arată că fiecare parte a centrului de masă al pendulului are două poziții pentru susținerea prismele în care perioadele de oscilație pendulului coincid.