Luați în considerare conceptul de frecvență critică rotație prin exemplul unui rotor simplu cu un singur disc, Fig. 2
Se compune dintr-un arbore de antrenare imponderabilitate elastic perfect rigid și perfect echilibrat. Deoarece rotorul este complet simetrică, considerăm doar deformarea acestuia în planul xy. În acest caz, poziția discului este descrisă prin două coordonate independente (coordonate x și q coordonatei) și avem un sistem cu două grade de libertate.
Proprietățile elastice maleabilitate arborelui descris coeficienți de matrice simetrice. Discul are o greutate și momentele respective de inerție.
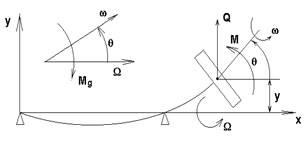
Fig. 1. Diagrama rotor cu un singur disc
Vibrațiile și rezistența rotorului este determinată de două tipuri de rotație. Primul tip - rotirea planul xy. în care axa arborelui este curbată în jurul unei axe care trece prin punctele de susținere a arborelui cu o viteză unghiulară W. Acest tip de mișcare circulară se numește precesiune axa rotorului elastic. II - o rotație corespunzătoare a rotorului (ax și disc) în jurul axei curbată a w vitezei absolute. Viteza W și W sunt independente, raportul dintre aceste două viteze poate fi arbitrară.
Trebuie să se înțeleagă că precesia are loc, de obicei, cu o frecvență egală cu cea a forței perturbator L. W = L.
Ca urmare a mișcării circulare a centrului de masă al discului în punctul de atașare disc la arborele are loc forță neechilibrată
unde m - masa discului; y - unitate de mișcare liniară.
Ca urmare, mișcarea de rotație complex de arborele de antrenare pentru a realiza un moment de încovoiere
unde Jd diametral momentul de inerție al discului; Jp - momentul de inerție polar al unității.
Primul termen este un moment de inerție a discului din mișcarea circulară a planului elastic axa arborelui, al doilea membru - momentul giroscopic. Formula poate fi scrisă ca
în cazul în care - adimensionale.
Coeficientul A este coeficientul de precesie, valoarea sa depinde de forma de precesiune prestabilita coeficient r s. E. Raportul dintre vitezele și W w.
Pentru a evalua stabilitatea rotorului este necesară pentru a determina eventuala existență a mișcării precesional a rotorului, în absența forțelor perturbatoare externe. Cu astfel de forțe interne și momente de mișcare arbore elasticitate pe deplin echilibrată care apar forțe de inerție și momente.
Condițiile în care este posibilă o astfel de precesie, sunt condițiile pierderii de rezistență a rotorului, ca arborele de capacitatea de transport devine zero.
Să presupunem că rotorul poate suferi pretsesionnoe libera circulație. devierea arborelui și rotația sub acțiunea forțelor de inerție și momentelor determinate de ecuațiile
în cazul în care a11. A12. Influența coeficienților A22 (conformitatea).
Înlocuirea forțelor și momentelor de valorile lor, conform formulei de mai sus obținem un sistem de două ecuații omogene
Aceste ecuații omogene au soluții diferite de zero, cu condiția ca determinantul coeficienților necunoscutelor acestor ecuații este egal cu zero:
Extinderea determinantul și substituind și obținem ecuația de frecvență
Rădăcinile sale (valorile W și s) definesc tipurile de precesie și valorile numerice ale vitezelor W și w. la care rotorul devine instabil.
În ecuația (8), valoarea depinde de forma de precesie. Pentru precesie sincron directă = 1. Pentru precesia sincron inversă = -1. Ecuația are un număr infinit de soluții, deoarece s poate lua orice valoare. Aceste soluții pot fi prezentate sub forma unor rapoarte de viteză diagrama W și w. (Graficul de frecvență), Figura 2.
În diagrama de frecvență, axa ordonatei poate fi amânată, L - frecvența forței perturbator.
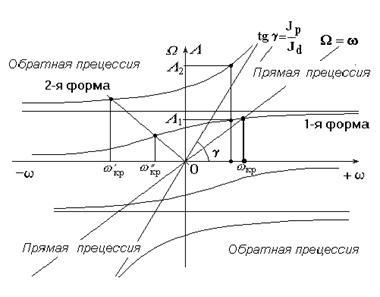
Fig. 2. Diagrama de frecvență rotor singur disc
Pentru a calcula frecvența naturală și construi poate lua următoarele valori. = 2; 1; 0,3; 0.0; -0.5; -1; -2. Înlocuind aceste valori în ecuația (8) și rezolvarea ei pentru fiecare tip de precesie obține frecvența naturală.
Pentru a găsi valorile vitezelor critice. necesitatea de a obține o valoare înmulțită cu. Apoi, este posibil să se construiască o diagramă de dependență
asimptotă orizontală obținută din condițiile
Ecuația pentru găsirea asymptotes înclinate
și anume asimptotă înclinat trece prin origine, la un unghi
coeficienților de influență pentru sistemul de rotor dat poate fi definit prin următoarele formule:
E - modulul de elasticitate al materialului arborelui;
J - momentul de inerție al secțiunii transversale a arborelui;
L1 - lungimea secțiunii în consolă a arborelui;
L - lungimea totală a arborelui.
graficul frecvenței de analiză conduce la următoarele elemente este concluzii foarte importante.
1. Frecvența naturală a oscilațiilor rotorului depinde de viteza rotorului. Acest fenomen se explică prin influența momentul giroscopic care apar în timpul rotației discurilor rotor.
2. rotorul poate acționa ca forțe externe și interne care apar în timpul rotației datorită dezechilibrelor reziduale. Pentru a proiecta un rotor cu activitate de vibrație scăzută, este necesar să se cunoască relația dintre frecvența forței de excitație, iar frecvențele de oscilații naturale.
3. În cazul în care frecvența forței de excitație coincide cu frecvența naturală a oscilațiilor rotor, are loc fenomenul de rezonanță, care este însoțită de vibrații mari - deturnări mari ale arborelui rotorului, sarcinile în lagăre.
4. Viteza rotorului, care coincide cu frecvența naturală de oscilație, numită frecvența critică de rotație, deoarece la această rezonanță apare viteza rotorului - frecvența de excitație a forței de dezechilibru coincide cu frecvența naturală de oscilație. Forțele neechilibrate au tendința de a provoca o precesie sincron directă.
5. Pentru a determina viteza rotorului la care apare rezonanță a sistemului, este necesar de origine să dețină fasciculul la un unghi la intersecția cu curbele de frecvențe naturale. Pentru a determina frecvența critică de rotație, atunci când. grindă a avut loc la un unghi de 45 de grade.
1. DV Hronin Fluctuațiile în motoarele de aeronave. - M. Inginerie Mecanică, 1980