
Acasă | Despre noi | feedback-ul
Această secțiune cuprinde materiale suplimentare cu privire la metodele de rezolvare a integralele specifice și improprii. Se presupune că cititorul are un mediu sau abilități înalte de integrare. Dacă nu, vă rugăm să începeți cu elementele de bază: The nedefinite integrale, exemple de soluții.
În cazul în care o integrală nedefinită - acolo apropiat și definit integrală. cu formula Newton-Leibniz, ar trebui să fie, de asemenea, la prima mână familiară. Mai mult decât atât, rezolva problema de calcul a formei plane pătrat (a se vedea. 7.2.3.) Și calcularea volumului corp de rotație (cm. 7.2.4.).
Lecția este conceput pentru cei care doresc să învețe cum să rezolve integralele definite și inadecvate mai rapid și mai eficient. În primul rând, ia în considerare caracteristicile integrării funcției pare și impare pe un interval simetric în jurul valorii de zero. Apoi, vom face cu problema de a găsi suprafața unui cerc folosind integrala definită. Acest obiectiv este de asemenea important ca te introduce tehnica comună de integrare a integrala definită - substituția trigonometrice. Ea nu a văzut - lucruri noi!
În mod similar, ia în considerare integralele improprii de chiar și funcții impare ale intervalului simetric. În special, mai multe tipuri rare de integralelor improprii, care nu sunt incluse în materialul de bază din secțiunile anterioare, în cazul în care limita inferioară tinde să „minus infinit“, atunci când ambele limite la infinit, atunci când ambele capete ale intervalului funcției de integrare suferă decalaj fără sfârșit (aceasta este o parte integrantă al doilea tip). Și este o parte integrantă improprie rară - un punct de discontinuitate în intervalul de integrare.
O metodă de rezolvare integrala definită a unei funcții chiar simetric în raport cu segmentul de zero
Luați în considerare integrala definită a formei
Este ușor de observat că intervalul de integrare [-c; c] este simetrică în raport cu zero.
Dacă integrantul f (x) este chiar. apoi integrala
Acesta poate fi calculată din jumătatea segmentului, iar rezultatul - dublu:
Mulți ghicit de ce acest lucru este așa, dar să considerăm un exemplu specific al desenului:
Calculați integrala definită
Despre funcția de paritate de mult a fost spus în graficele materiale metodice și proprietățile funcțiilor elementare. Încă o dată: este o funcție chiar, în cazul în care egalitatea f (-x) = f (x) pentru ea.
Cum de a verifica funcția pe paritate? Avem nevoie de vmestox înlocui -x.
În acest caz: și.
Deci, această funcție este chiar.
Conform regulii, simetrice în jurul intervalului de zero [-2; 2], parte integrantă a noastră o funcție chiar și poate fi calculată după cum urmează:
Acum, interpretare geometrică. Da, vom continua să chinuiască parabolei nefericit ....
Orice funcție chotnaya în particular. simetrice în raport cu axa OY:
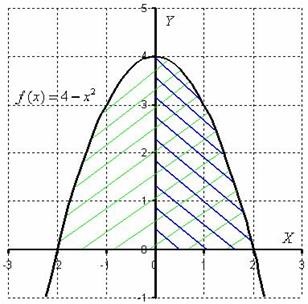
numeric egală cu aria unei figuri plan care este umbrită în verde. Dar, din cauza parității integrandul, și, în consecință, simetria programului său în raport cu axa OY. suficiente pentru a calcula aria figurii, albastru umbrită, iar rezultatul - dublat. jumătăți identice este un proprietăți de expresie geometrice ale paritate. Acesta este motivul pentru care efectul real
O poveste similară are loc cu orice funcție chiar f (x) pe intervalul simetric în raport cu zero:
Unii vor spune: „Dar de ce toate acest lucru este necesar, pentru că poți, și așa mai departe calcula integrala definit.“ Posibil. Să se calculeze:
Dar dacă era convenabil să înlocuiască o limită inferioară negativă? Nu foarte mult. Apropo, un procent de zero a studenților fac o greșeală în semne. Este mult mai ușor și zero, substitut mai plăcută. Rețineți că acest lucru a fost încă o demonstrație simplă, în practică, totul este mai rău.
Mai mult decât atât, raportarea de recepție este adesea utilizat la calcularea integralele duble. Integrale triple. în cazul în care de calcul și așa mai lipsesc.
exemplu scurt pentru soluțiile independente:
Calculați integrala definită
Soluții complete și răspunsuri la sfârșitul lecției.
Vă rugăm să rețineți că, atunci când vi se cere să se calculeze o integrală definită, nu sunt necesare desen! Figura 1 prezintă, de exemplu, numai pentru ao face regulă clară. Doar de data aceasta dedicat următoarea sarcină simplă:
3.1. Calculați integrala definită
3.2. Se calculează aria unei figuri plane delimitate prin linii
. și axa OX la interval.
Acestea sunt două probleme diferite! În primul rând, să se ocupe cu primul punct:
1) integrandul este chiar, intervalul de integrare este simetrică în raport cu zero, astfel:
Definite integrală a fost negativă și acest lucru se întâmplă!
Acum vom găsi zona unei figuri plane. Aici, fără un plan de a gestiona dificil:
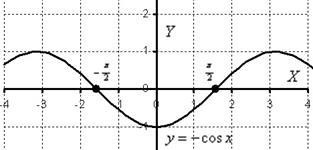
Pe graficul segmentului este situat sub axa OX. Prin urmare:
Zona nu poate fi negativ, de aceea, în formula se adaugă minus calculul suprafață (vezi. De asemenea, Exemplul 3 din secțiunea 7.2.3.).
Rețineți că cosinusul paritate nu a fost anulat, asa ca am impartit din nou intervalul și dublat integrală.