Diversitate.
grafice izomorfe.
Rețineți că graficul G (Fig. 1), poate fi reprezentat în diferite moduri.
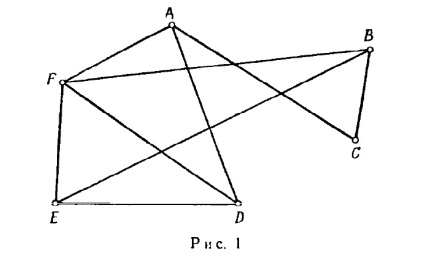
În primul rând, nu este necesar să se reprezinte drept muchiile sale. Putem efectua orice linii de legătură între aceleași vârfuri ca și înainte. De exemplu, un grafic G poate fi reprezentată așa cum este prezentat în Fig. 7.
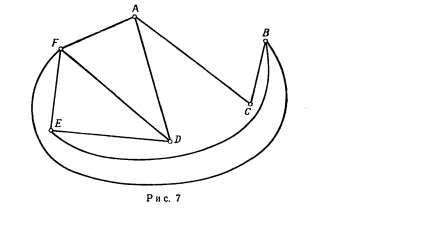
În al doilea rând, putem plasat în mod arbitrar pe partea de sus a planului. De exemplu, nodurile G pot fi poziționate după cum se arată în Fig. 8.
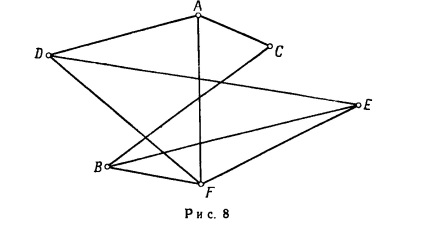
Dacă luăm în considerare cele trei graficele prezentate în Fig. 1, 7 și 8, ca și graficele care descriu cursul evenimentului sportiv, acestea vor conține exact aceleași informații ca și la ce fel de echipa au jucat unul cu celălalt; într-un sens, este același grafic. Vom vorbi. două grafa- G1 și G2 reprezintă lor - izomorfe dacă îndeplinesc aceeași listă de jocuri jucate. Cu alte cuvinte, în cazul în care G1 și G2 grafice sunt izomorfe. ei au același număr de noduri și oricare două vârfuri ale graficului G1, spun B1 și C1, sunt conectate printr-o muchie noduri B2 și C2 grafic G2 este, de asemenea, conectate printr-o muchie și spate corespunzătoare.
Conform acestei definiții, cele trei graficele din Fig. 1, 7 și 8 sunt izomorfe (de ex., E. au aceeași structură), chiar dacă acestea arata diferit.
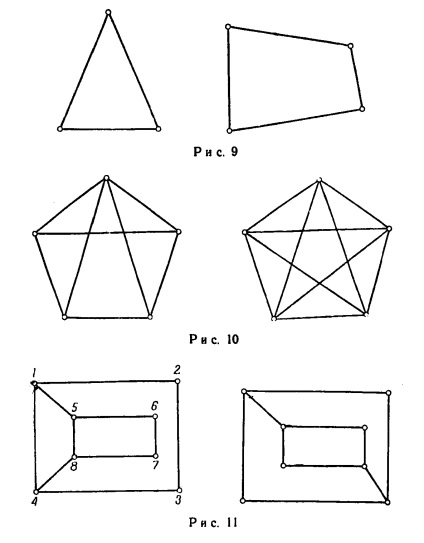
De multe ori trebuie să decidă problema dacă cele două date graficului izomorfe. Uneori este imediat clar că acest lucru nu este așa. De exemplu, graficele prezentate în Fig. 9, nu poate fi izomorfe, deoarece acestea au un număr diferit de noduri. Este posibil să nu fie izomorfe și graficele din Fig. 10, deoarece acestea au un număr inegal de margini.
Cu toate acestea, pentru a arăta că nu este izomorfă graficele prezentate în Fig. 11 este necesar pentru unele argumente mai subtile. Astfel, se poate observa că prima coloană are o secvență de opt muchii adiacente (adică marginile în perechi având un vârf comun ..): (1,2), (2,3), (3,4), (4,8 ), (8,7), (7,6), (6,5), (5,1), revenind la vertex inițial, în timp ce nici o astfel de secvență în a doua coloană. Deci, indiferent de modul în care vom nota nodurile al doilea grafic, nu putem pentru fiecare pereche de noduri conectate printr-o margine a graficului indică a doua pereche corespunzătoare de noduri conectate printr-o margine, de asemenea.
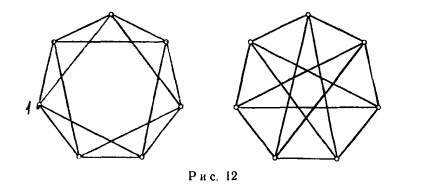
Dacă pur și simplu nu se poate vedea cum să dovedească faptul că cele două grafice nu sunt izomorfe, atunci problema izomorfism lor poate fi destul de dificil. Ca un exemplu, ia în considerare cele două grafice prezentate în Fig. 12; aceste grafice de fapt izomorfe.