
Acasă | Despre noi | feedback-ul
Odată cu construirea ecuației de regresie fiind evaluată apropierea conexiunii
între fenomenele (între variabile).
etanșeitate Conexiune în caz de dependență liniară se caracterizează prin
proba coeficientul de corelare rxy
Selective rxy Coeficientul de corelație este asociat cu un raport de regresie liniară Coeficientul b
Cu cât valoarea rxy a unității, cu atât mai îndeaproape o relație liniară, și cu atât mai bine relația liniară este în concordanță cu datele observate. Când rxy = 1 link devine funcțional, t. E. Raportul este efectuată pentru toate observațiile.
Când rxy> 0 este o legătură directă, cu rxy <0 – обратной.
Ecuația de regresie liniară, precum și un indicator de funcție liniară completate de etanșeitate relații între variabile. și anume indicele de korrelyatsiiR
Valoarea acestui indice este în limitele; apropierea de una, mai aproape legătura dintre aceste simptome, găsită mai fiabil ecuația de regresie.
Studii economice este larg utilizat un indicator, cum ar fi coeficientul de elasticitate, în special, coeficientul mediu de elasticitate.
Coeficientul mediu de elasticitate indică procentul valorilor factorului agregat medii x modificări y rezultă din valoarea medie a acestora atunci când schimbă factorul x este de 1%:
Pentru o funcție liniară:
Măsura totală a calității generale a ecuației de regresie (ecuațiile corespunzătoare
Statisticile regresiei) este determinarea coeficientului de R2.
În cazul aburului coeficientul de regresie de determinare va coincide cu pătratul coeficientului de corelație:
În general, coeficientul de determinare calculat cu formula:
Să ne explicăm semnificația coeficientului de determinare. Să ecuația de regresie empirică este:
Apoi a observat (reală) valoarea yi. i = 1, 2, .... n, modelul yi diferă de suma EI:
Această din urmă relație poate fi rescrisă după cum urmează:
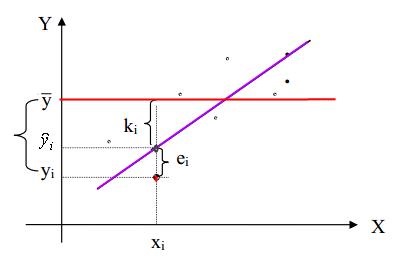
în care - i -lea deviație (observate) în ceea ce privește valoarea medie a variabilei dependente Y;
- o abatere de la punctul i-lea pe linia de regresie de la;
- o abatere de la punctul i-lea a valorii modelului. măsurată prin linia de regresie.
Toate deviațiile sunt calculate pentru axa variabilă dependentă (vezi. Fig. 3.3).
Ridicați ambele părți ale ecuației (*) în piață și suma valorilor care rezultă din volumul eșantionului n:
Se poate demonstra că (dovada este omis pentru exercitarea). Apoi, avem următoarea relație:
- total (complete), suma pătratelor (poate fi interpretată ca o măsură comună de răspândire (dispersie) în raport cu Y variabilă). (TSS)
- Explicarea suma pătratelor, interpretată ca o măsură de răspândire, explicabilă printr-o regresie. (SSE)
- reziduală (inexplicabilă) suma pătratelor, care este o măsură a ecartului reziduală, neexplicată ecuație de regresie (răspândirea punctelor în jurul liniei de regresie). (RSS)
Împărțind (3.13) pe partea stângă a acestuia, obținem:
Introducerea notația. obține (3.12). Este evident că coeficientul de determinare R 2 determină cantitatea de variație a variabilei dependente, regresia explicabile Y pe X.
definește fracțiunea de dispersie variabilă dependentă, regresia inexplicabilă a Y pe X.
Din considerentele de mai sus rezultă că, în general, relația 0 ≤ R2 ≤ 1.
Coeficientul de determinare R 2 este o măsură pentru a determina amploarea găsită de linia de regresie oferă cele mai bune rezultate pentru explicarea comportamentului dependent Y variabilă, decât orizontale = linia Y.
Prin urmare, cu cât relația liniară între X și Y, cu cât coeficientul de determinare R 2 la unitate. Este mai slab această conexiune, R 2 este mai aproape de zero.