Definiția. Seria numerică este o expresie
.
Numărul u1, u2, u3; ...; ONU; ... se face referire la o serie de numere de membri și
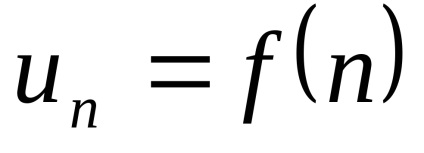
Definiția. Suma primilor n termeni ai seriei se numește suma parțială n-lea al seriei și este notată cu Sn. care este
În special: S1 = u1, S2 = u1 + u2, S3 = u1 + u2 + u3 etc. Sumele parțiale ale formei secvenței numerice
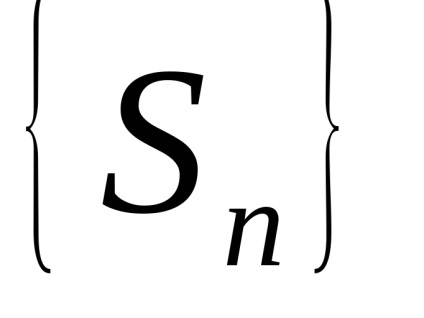
Definiția. Suma S a seriei număr se numește limită a secvenței de sume parțiale
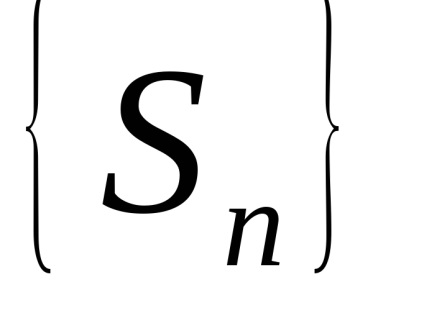
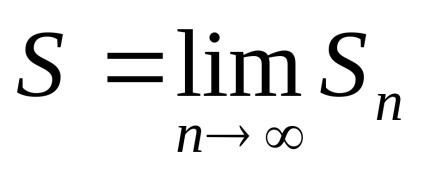
Seria numerică se numește convergentă. dacă are valoarea (în acest caz, există o limită finită sume parțiale ale secvenței) și divergente. în cazul în care acest lucru nu există (
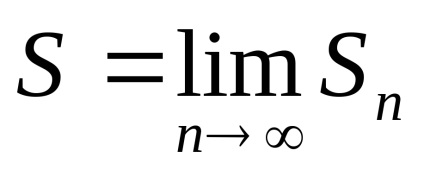
În cazul în care numărul seriei
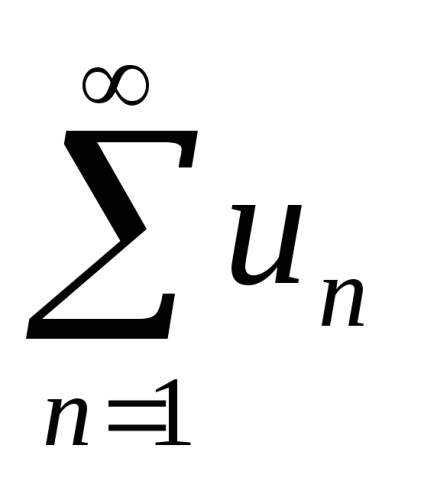
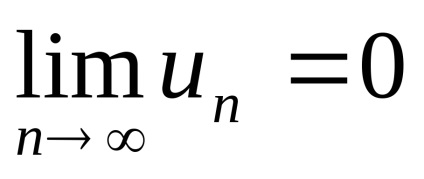
Criteriul de convergență Având în vedere trebuie înțelese după cum urmează:
dacă
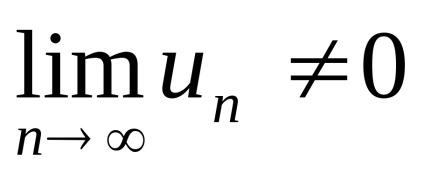
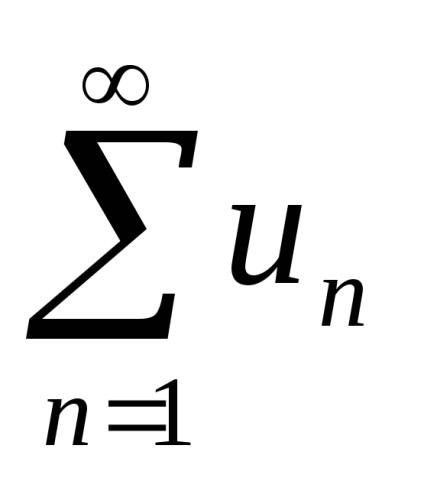
dacă
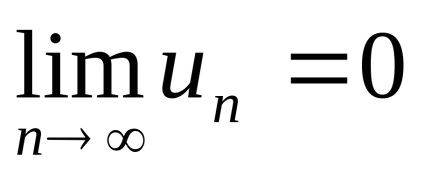
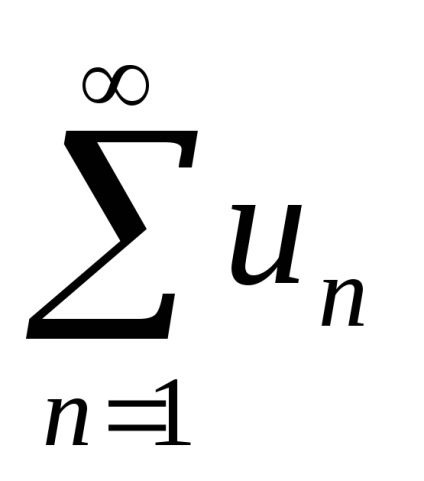
convergență semne suficiente de serii pozitive
comparație semn 1
două serii znakopolozhitelnyh Să presupunem că
în care numărul de membri (1) nu depășește numărul corespunzător de membri (2), cel puțin de la un indice n = N. care este
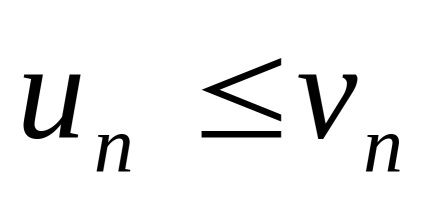
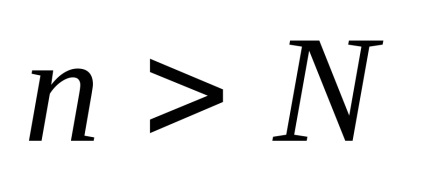
convergența seriilor (2), și urmează întotdeauna convergența seriilor (1),
de divergență a seriei (1) urmează întotdeauna raskhoimost serie (2).
semn compararea 2 (limitarea)
Dacă există o limită finită, relațiile de zero
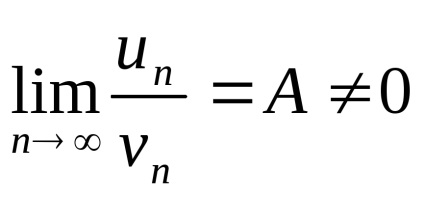
În aplicarea numărului de comparații caracteristică este asociat cu unul din așa-numita serie de referință, convergența sau divergența care este stabilită.
serii de referință
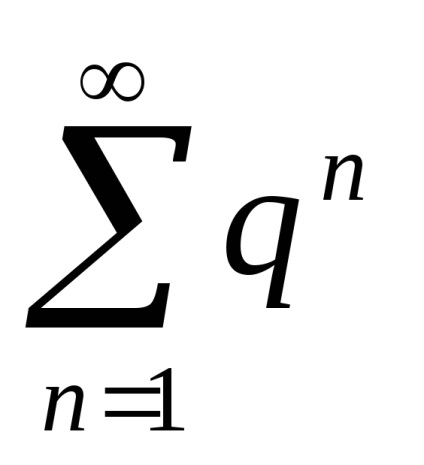
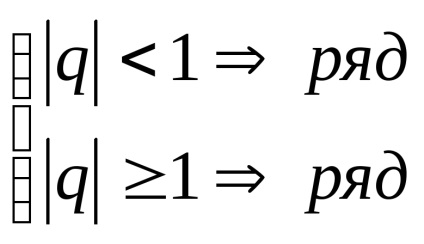
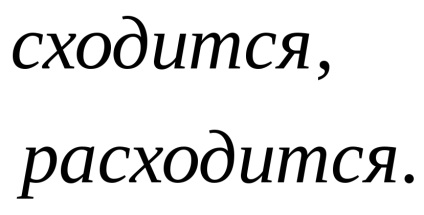
Seria armonică generalizată
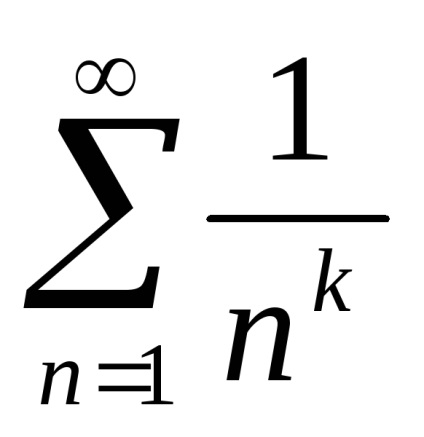
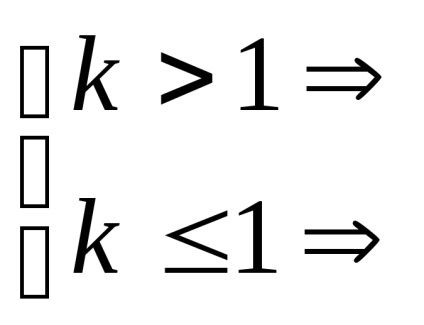
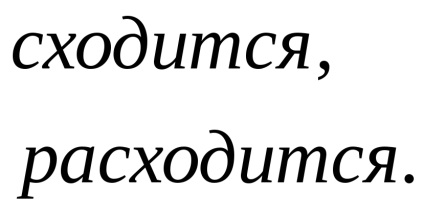
În special, pentru k = 1, obținem