În 7 și clasele a 8-ați studiat unele proprietăți ale funcțiilor. Acum le-am aduna împreună într-un singur paragraf, ne amintim esența lor și semnificația geometrică și sunt de acord asupra ordinea în care vom enumera aceste proprietăți la citirea funcției graficului. Notă: toate definițiile Featured set de numere X, care face parte din domeniul funcției: X la D (f). În practică, cele mai multe ori există cazuri în care X - numărul de timp (interval, intervalul, grinzi, etc.).
Funcția y = f (x) este numit pentru creșterea setului X cu D (f), în cazul în care pentru oricare două puncte x1 și x2 sunt setate X, astfel încât x1 <х2. выполняется неравенство f(х1
Funcția y = f (x) este numit pentru descreșterea setului X cu D (f), în cazul în care pentru orice monotonie două puncte x1 și x2 sunt setate X, astfel încât x1 <х2. функции выполняется неравенство f(x1 )> f (x2).
În practică, este mai convenabil să se folosească următoarea formulare: funcție este crescută în cazul în care o valoare mai mare a argumentului corespunde unei valori mai mari a funcției; Funcția scade dacă valoarea mai mare a argumentului corespunde valorii minime a funcției.
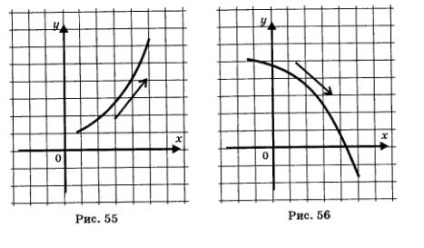
In 7 si 8 grade, am folosit următoarea interpretare geometrică a conceptului de creștere sau descreștere funcții: se deplasează asupra funcției crescătoare program de la stânga la dreapta, ca și în cazul în care vom urca dealul (figura 55.); se deplasează asupra funcției descrescătoare program de la stânga la dreapta ca și în cazul în care merge în jos un deal (fig. 56).
De obicei, termenii „funcția de creștere“, „funcția de scădere“ este numele general al unei funcții monotonă, și funcțiile de cercetare pentru a mări sau micșora menționate la studiul privind funcția de monotonie.
Rețineți, de asemenea una circumstanță: când crește funcție (sau scade) în domeniul său natural, se spune în general că funcția de creștere (sau descreștere) - fără a specifica un X. pluralitate numerică
Investigarea pentru monotonia funcției:
a) y = x 3 + 2; b) y = 5 - 2.
a) vor lua arbitrar valori argument x1 și x2, și lăsați x1 <х2. Тогда, по свойствам числовых неравенств (мы с вами изучали их в курсе алгебры 8-го класса), будем иметь:
Ultima inegalitate înseamnă că f (x1)
Funcția y - f (x) se numește mărginită de jos printr-un set de X la D (f), în cazul în care toate valorile funcției pe mulțimea X mai mare decât un anumit număr (cu alte cuvinte, în cazul în care există un număr m astfel încât pentru orice valoare a lui x ∈ X satisface inegalitatea f ( x)> m).
Funcția y = f (x) se numește o limită superioară setului X cu D (f), în cazul în care toate valorile mai puțin de un anumit număr (cu alte cuvinte, în cazul în care există un număr N astfel încât pentru orice valoare a lui x ∈ X satisface inegalitatea f (x) <М).
În cazul în care X nu este specificat, se presupune că aceasta este o limitare a funcției de mai jos sau mai sus de-a lungul domeniului.
În cazul în care funcția este limitată, iar partea de jos și de sus, atunci aceasta se numește limitată.
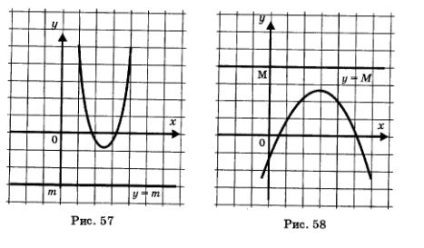
Limitele funcțiilor pot fi ușor de citit pe programul ei. în cazul în care funcția este delimitată sub graficul ei se întinde în întregime deasupra unei linii orizontale y = m (Fig 57.); dacă funcția este mărginită de mai sus, graficul acesteia se întinde în întregime sub o linie orizontală y = M (fig. 58).
Exemplul 2. Testarea funcției limitate
Decizie. Pe de o parte, este destul de evident inegalitate (astfel cum sunt definite de rădăcina pătrată a ceea ce înseamnă că funcția este mărginită de mai jos. Pe de altă parte, avem, prin urmare,
Acest lucru înseamnă că funcția este mărginită de sus. Acum, uita-te la funcția graficului dat (fig. 52 din secțiunea anterioară). Funcțiile și limitările de sus și de jos a graficului este citit destul de ușor.
Numărul m este cea mai mică valoare a funcției y = f (x) pe multimea X C D (f), în cazul în care:
1) X există un x0 punct. că f (x0) = m;
2) pentru toate x din X satisface inegalitatea m> f (x0).
Numărul M este declarat cea mai mare valoare a funcției y = f (x) pe multimea X C D (f), în cazul în care:
1) X există un x0 punct. că f (x0) = M;
2) pentru toate x din inegalitatea X
Cea mai mică valoare a funcției a fost notată în clasele 7 și 8 în simbol, iar cel mai mare - în simbol.
În cazul în care X nu este specificat, se înțelege că este vorba despre găsirea cea mai mică sau cea mai mare valoare a funcției în întregul domeniu.
Destul de evident următoarea afirmație utilă:
1) În cazul în care există o funcție de Y, atunci este mărginită de mai jos.
2) Dacă există o funcție de Y, atunci este mărginită de mai sus.
3) Dacă funcția nu este mărginită de mai jos, atunci Y nu există.
4) Dacă funcția nu este mărginită de mai sus, atunci Y nu există.
Găsiți cele mai mici și cele mai mari valori ale funcției
Decizie.
Este suficient de clar, mai ales dacă se recurge la graficul funcției (Fig. 52), care a = 0 (această valoare este atinsă la punctele x = -3 și x = 3), a = 3 (această valoare este atins în punctul x = 0.
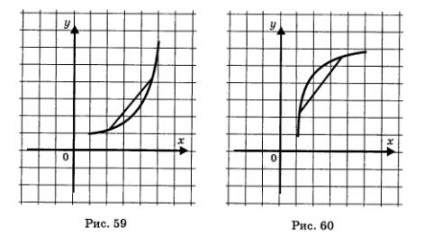
In clasele 7 si 8, am menționat două proprietăți ale funcțiilor. Proprietățile mai întâi cu numele de funcții convexe. Se crede că funcția este convexă în jos, în intervalul X, în cazul în care, prin conectarea oricare două puncte ale graficului său (cu abscise de X) segment de linie, constatăm că partea corespunzătoare a graficului se află sub realizată de segmentul (Fig. 59). continuitatea funcției este convexă în sus pe intervalul X, dacă funcția de conectare oricare două puncte ale graficului său (cu abscise de X) segment de linie, constatăm că partea corespunzătoare a graficului este deasupra segmentului efectuat (Fig. 60).
A doua proprietate - continuitatea funcțiilor de pe X - este că graficul funcției pe intervalul X - un solid, adică, Ea nu are puncții și salturi.
De fapt, totul este în matematică, așa cum se spune, „exact opusul“: graficul functiei reprezentat de linia solidă (fără puncții și sare) numai atunci când dovada continuității funcției. Dar definiția formală a continuității unei funcții, este destul de complicată și delicată, nu am fost în stare să facă. Același lucru se poate spune despre convexitatea funcției. Discutând aceste două proprietăți ale funcțiilor, vom continua să se bazeze pe idei vizuale-intuitiv.
Acum dețin vedere cunoștințele noastre. Amintindu acele funcții pe care le studiază în clasele 7 si 8, rafina aspectul lor grafice, și lista proprietățile funcției prin aderarea la o anumită ordine, cum ar fi acest lucru: domeniu; monotonie; limitări; . ; continuitate; interval de valori; umflatura.
Ulterior, vor exista noi proprietăți ale funcțiilor vor varia în mod corespunzător și lista proprietăților.
1. Funcția permanentă y =
Graficul funcției y = G prezentată în Fig. 61 - linie paralelă cu axa x. Este atât de caracteristică neinteresantă este că nu are nici un sens pentru a enumera proprietățile sale.
Graful y = kx + m este o linie dreaptă (Fig. 62, 63).
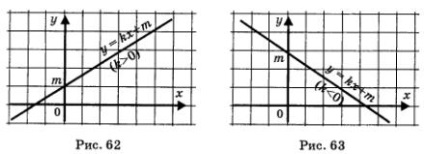
Proprietățile funcției y = kx + m:
1)
2) crește, în cazul în care k> 0 (fig. 62), scade dacă k <0 (рис. 63);
3) de mai jos nu este limitată la audio, semnalul audio de mai sus;
4) nici un maxim sau minim valori;
5) este continua;
6)
7) nervurii spunând că nu are nici un sens.
Graficul funcției y = kx 2 este o parabolă cu vârful la origine și cu ramurile îndreptate în sus, dacă k> (Fig. 64), și în jos, în cazul în care k <0 (рис. 65). Прямая х = 0 (ось у) является осью параболы.
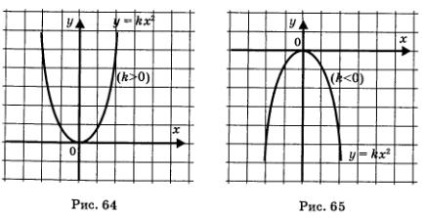
Proprietăți ale funcției y - k, 2:
Pentru cazul k> 0 (Figura 64.):
1) D (f) = (-∞, + ∞);
2) scade raza (-OO, 0], este mărit cu raze din [0, + ∞);
3) limitate de jos, nu este mărginită de mai sus;
4) nu = activ;
5) continuu;
6) E (f) = [0, + ∞);
7) este convexă.
Notă: în intervalul (-OO, 0] funcția scade, iar pe intervalul [0, + oo) crește. Aceste intervale sunt numite intervale de monotonia funcției y = kx 2. Conceptul monotoniei diferenței vor fi utilizate pentru alte funcții.
Pentru cazul la <0 (рис. 65):
1) D (f) = (-∞, + 00);
2) crește de-a lungul liniei (-OO, 0], scade raza de [0, + ∞);
3) nu delimitate de mai jos, mărginită de mai sus;
4) nu există, = 0;
5) continuu;
6) E (f)> = (-OO, 0];
7) este convex în sus.
Graficul funcției y = f (x) pe puncte; Cu cat mai multe puncte ale formularului (x; f (x)) vom lua, reprezentarea mai precisă a graficului obținem. În cazul în care aceste puncte pentru a lua destul de mult, iar ideea de a parcelei se va dezvolta mai mult pe deplin. În acest caz, intuiție, și ne spune că programul ar trebui să fie reprezentat ca o linie solidă (în acest caz, sub forma unei parabole). Și apoi citirea graficului, vom face concluzii cu privire la continuitatea funcției, convexitate sale în sus sau în jos pe valorile de câmp ale funcției. Trebuie să realizezi că aceste șapte proprietăți „legitime“ sunt doar proprietăți 1) 2) 3) 4) - „legală“, în sensul că suntem capabili să le susține, referindu-se la definițiile exacte. Pe celelalte proprietăți avem idei doar vizual-intuitiv. Apropo, nu este nimic în neregulă cu asta. Din istoria matematicii cunoscute omenirii pentru o lungă perioadă de timp și de multe ori folosesc diferite proprietăți ale diferitelor obiecte fără a cunoaște definițiile precise. Apoi, când o astfel de determinare a fost în măsură să formuleze, totul se încadrează în loc.
Graficul funcției este o hiperbolă, coordonatele sunt axele asimptote ale hiperbolă (Fig. 66, 67).
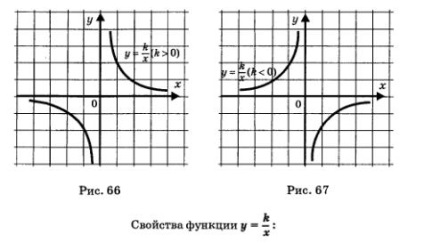
1) D (f) = (-00,0) 1U (0, + ∞);
2) în cazul în care k> 0, apoi scade în raza deschis (-OO, 0) și raza deschis (0, + ∞) (Figura 66) .; în cazul în care un <0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);
3) de mai jos nu este limitată la audio, semnalul audio de mai sus;
4) Nu sunt mai mici sau mai mari valori;
5) este continuă în raza deschis (-OO, 0) și raza deschis (0, + ∞);
6) E (f) = (-OO, 0) U (0, + ∞);
7) În cazul în care k> 0, atunci funcția este convexă în sus atunci când x <0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х> 0; ray în aer liber (0, + ∞) (Fig. 66). În cazul în care un <0, то функция выпукла вверх при х> O și convex în jos la x <О (рис. 67).
5. funcţia
Graficul unei funcții este o ramură a parabolei (fig. 68). proprietăți funcționale:
1) D (f) = [0, + ∞);
2) crește;
3) limitate de jos, nu este mărginită de mai sus;
4) nu = activ;
5) continuu;
6) E (f) = [0, + ∞);
7) este convex în sus.
Graficul funcției este de a reuni cele două fascicule:
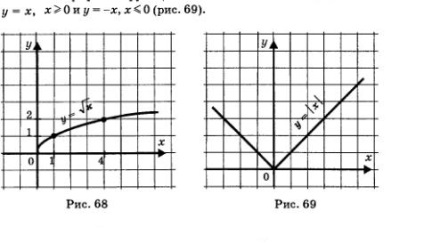
Proprietățile funcției y = | x |:
1) D (f) = (-∞, + ∞);
2) scade raza (-OO, 0], este mărit cu raze din [0, + ∞);
3) limitate de jos, nu este mărginită de mai sus;
4) nu = activ;
5) continuu;
6) E (f) = [0, + ∞);
7) o funcție poate presupune o convexă în jos.
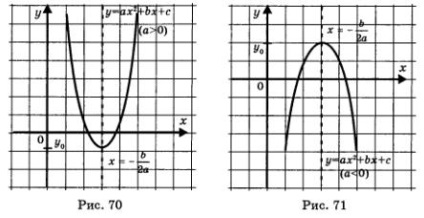
7. Funcția y = ax 2 + bx + c
Graficul unei funcții este o parabolă cu vârful în punctul
și ramurile îndreptate în sus, atunci când un> 0 (fig. 70), și în jos,
în cazul în care un <0 (рис. 71). Прямая является осью параболы.
Examinați cunoștințele noastre despre funcțiile pot fi considerate complete. Desigur, lista de mai jos nu se poate face în viața reală. Unele dintre noile caracteristici și proprietăți pentru a ne întâlni deja în acest capitol.
Materiale în matematică online. provocări și răspunsuri pe clasă, planuri de lecție, note de curs în matematică descărcare
Dacă aveți corecturi sau sugestii la această lecție, vă rugăm să ne contactați.
Dacă doriți să vedeți alte ajustări și sugestii pentru lecții, uita-te aici - Forumul Educațional.