Să o y funcție = f (x), definită pe un set de valori argument D.
Funcția y = f (x) se spune mărginită pe D, în cazul în care există un număr pozitiv M, astfel încât pentru toate valorile x din setul considerat, inegalitatea | f (x) | ≤M. În cazul în care acest număr M nu există, atunci f funcția (x) este chemat să stabilească nelimitat D.
exemplu:
Funcția y = sin x, definit pentru -∞
Dacă funcția f (x) are o limită de la punctul A, este limitată într-un cartier al unui.
dovada:
Să. atunci. aici
Noi primim. Reciproca nu este adevărat.
Cazul de testare:
într-un cartier de la 0.
- nu există.
Infinitezimală și proprietățile lor.
Funcția y = f (x), se spune infinitezimale x → a, sau când x → ∞, dacă oricare. și anume Funcția infinitezimal - o funcție, în care limita la acest punct este zero.
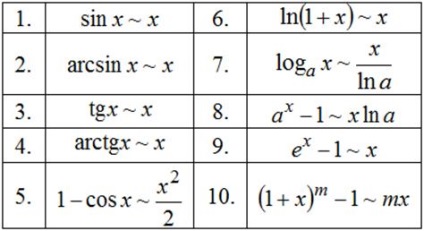
- Funcția f (x) = (x-1) 2 este infinitezimal când x → 1, din moment (vezi. Fig.).
- Funcția f (x) = TGX - infinitezimal la x → 0.
- f (x) = ln (1 + x) - infinitezimal la x → 0.
- f (x) = 1 / x- infinitezimal când x → ∞.
Proprietățile de bază ale funcțiilor infinitezimale (BM)
1 ° sumă a unui număr finit de infinitezimal Funcția este o funcție de infinit de mic.
2 ° Produsul utilizat pentru o funcție limitată este o funcție infinitezimal.
3 ° Produsul a două funcții este o funcție de BM infinitezimal ..
4 ° Funcția BM produs este o infima funcție constantă.
5 ° câtul funcției BM la o funcție a cărei limită nu este zero, funcția este infinit de mic.
6 ° funcție. funcție inversă BM. este o funcție de infinit de mare. Opusul este adevărat.
Teoreme de bază despre limite.
Teorema 1. Limita sumei este egală cu suma limitelor în cazul în care
sunt:
dovada:
Din relația dintre teorema limită și infinitezimal urmează:
obține
produs Teorema 2. Limita este egală cu produsul dintre limitele, în cazul în care acestea există:
dovada:
Din relația dintre teorema limită și infinitezimal urmează:
Ia-Teorema 3. Limita unui coeficient este egal cu exteriorul privat :. la
Stare: Există Toate limitele.
dovada:
Din relația dintre teorema limită și infinitezimal urmează:
;
obținem:
4. Limita Teorema păstrează semnul inegalității. În cazul în care.
dovada:
Prin urmare,
consecință:
Teorema 5. Dacă funcția este monotonă și este limitat la (a, b), are o limită:
20-21. Primul și al doilea limite și consecințe remarcabile.
Limita remarcabilă Teorema.Pervy.
Dovada (geometric):
Corolarul Teorema:
1)
2)
3)
4)
5)
Teorema.Vtoroy limita remarcabilă.
dovada:
Teorema binom:
. în cazul în care.
Noi folosim teorema binomială pentru a dovedi inegalitatea:
Concluzionăm că. asa.
Corolarul Teorema:
1)
2)
3)
4)
22. Comparațiile infinit malyhvelichin (b.m.v.) infinitezimal echivalent.
Să - cantități infinitezimale la. și anume .
Definiția 1. În cazul în care. apoi - b.m.v. aceeași ordine.
Definiția 2. În cazul în care. apoi - b.m.v. un ordin mai mare decât.
- un ordin mai mare decât ( „o“ - citește ca „un pic“).
- un ordin mai mic decât ( „O“ - citește „mare“).
3. În cazul în care definiția. și echivalentul -.
Corolar 3 din definiția: Teorema. Dacă echivalent (). și dovada:
Să - cantități infime atunci când acestea sunt echivalente).
Apoi.
BM funcționa și sunt echivalente sau echivalent cu BM la o comandă. dacă
Reprezentați. la.
Funcția de continuitate. Definiția de continuitate la un punct și pe un interval. Teorema privind operațiile aritmetice asupra funcțiilor continue. Continuitatea functiilor complexe. funcții continue. mărginite
Funcția care este continuă la toate punctele de unele regiuni, se numește continuă în acest domeniu.
Funcția se numește continuă pe dreapta la punctul. în cazul în care.
Funcția se numește continuă pe stânga la punctul. în cazul în care.
Funcția se numește continuă în intervalul. în cazul în care este continuă în fiecare punct al intervalului.
Funcția se numește continuă pe intervalul. în cazul în care este continuă în intervalul. continuă pe dreapta la punctul. atunci există continuu de pe stânga la punctul. adică.
Teorema privind operații aritmetice:
Dacă funcția f (x) - continuă în t x0 .. j (x) este continuă în m. x0. atunci:
1) f (x) ± j (x) - o funcție m x0 continuă ,.
2) f x j - o continuă funcție m x0 ,.
3) f / j, j (x0) ¹0 - continuu t x0 ..
26. Weierstrass teorema despre funcțiile limitate pe un interval închis.
1) În cazul în care funcția este continuă pe intervalul, acesta ajunge la acest punct, în maxim și valorile minime.
Și Imaginile din Figura
funcția interval este continuă și are valoarea sa maximă la un punct M. iar cea mai mică m - vtochke. Pentru orice inegalitate :.
2) Dacă funcția este continuă pe intervalul. este limitată la acest interval, adică există o constantă astfel încât
Teorema 27. Bolzano Cauchy a funcției valoare intermediară.
În cazul în care o funcție continuă definită pe intervalul real, are două valori, primește și orice valoare între acestea.
Corolar teoremei Bolzano-Cauchy
1. Teorema la zero a unei funcții continue.
Dacă funcția este continuă la un anumit interval, iar la capetele acestui segment ia valori de semne opuse, atunci există un punct la care valoarea funcției este zero.
2. În special, orice grad polinom impar are cel puțin un zero.
28. Determinarea funcției inverse. Teorema privind continuitatea funcției inverse.
Definiția. Lăsați funcția y = f (x) cu domeniul D (f) și o multitudine de R (f) valori. Feedback la f - funcția f-1 este definit ca o funcție cu domeniul D (f-1) = R (f) și valorile prescrise ale R (f-1) = D (f). astfel încât f-1 (y) = x dacă și numai dacă f (x) = y. Astfel, f-1 se întoarce înapoi la y x.
exemple:
Găsiți funcție inversă y = 3x + 5.
Soluție: Funcția y = 3x + 5 este definit și crește pe întreaga axă. Prin urmare, funcția inversă există și crește. Rezolvarea ecuației pentru x, obținem x = (y-5) / 3.
Arătați că funcția y = kx, în cazul în care (k ≠ 0) înapoi la sine.
Soluție: Funcția y = kx definită și monotonă în întreaga axă reală cu excepția punctului x = 0. Prin urmare, există o funcție inversă. valorile funcției FIELD - toate axele reale cu excepția punctului y = 0. Rezolvarea ecuației pentru x, obținem x = k / y.
Teorema privind continuitatea funcției inverse:
Dacă strict crescătoare (descrescătoare) pe. apoi pentru a defini funcția. care este inversul. continuă pe și strict în creștere (descreștere) pe.
dovada:
Să presupunem că funcția este strict crescătoare pe intervalul.
Potrivit anchetei funcțiilor din regiune a unei valori funcții continue, de asemenea, un decalaj.
Din cauza funcției stricte în creștere pentru fiecare există un punct unic, astfel încât.
Prin urmare, funcția are o funcție inversă definită pe intervalul și valorile setate.
Să ne arate că este strict crescătoare pe.
Să presupunem că - două puncte de la. cum ar fi prototipurile acestor puncte sunt punctele și. și.
Pentru că - în creștere strict funcție, atunci inegalitatea este posibilă dacă și numai în cazul în care aceeași sau când.
Având în vedere arbitrariului, putem concluziona că funcția - este strict crescătoare pe platoul de filmare.