Dacă problema dată perpendiculara dintr-un punct de pe circumferința diametrului său, să dau seama cum să împartă diametrul perpendicular, și pentru a găsi o legătură între segmentele rezultate și lungimea perpendiculare, trebuie să completați construcție suplimentară.

Să AB - diametrul cercului C - punctul cercului și CD - perpendiculara trasată de la punctul C la diametrul.
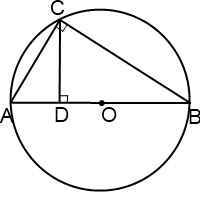
Conectați punctul C la diametrul capetelor. drepte (ca în funcție de diametru) - unghiul ACB. Prin urmare, ABC triunghi - pătrat, iar CD-ul în ea - înălțimea trase la ipotenuzei.
Acesta urmează perpendicular pe segmente de linie CD și BD și AD, pe care le împarte cu diametrul - segmente proporționale într-un triunghi dreptunghic. Acest lucru înseamnă că acestea sunt legate de:
În plus, triunghiul ABC
Perpendicular a scăzut de la un punct de pe circumferința diametrului său, diametrul împarte în segmente a căror diferență este egală cu 21 cm. Găsiți raza cercului dacă perpendicular 10 cm lungime.

Desenați segmente de linie de curent alternativ si BC.
∠ = 90 ° ACB (ca un unghi inscris subîntins de diametru). Apoi, într-un triunghi dreptunghic ABC CD - înălțimea trase la ipotenuzei. prin urmare
Să AD = x cm, iar BD = x + 21cm. Echivaleaza cu:
Cuadratura ambele părți:
A doua rădăcină - outsider, deoarece lungimea segmentului nu poate fi negativă. Prin urmare, diametrul AB = AD + BD = 4 + 4 + 21 = 29cm, iar raza egală cu jumătate din diametrul, adică r = 14,5sm.