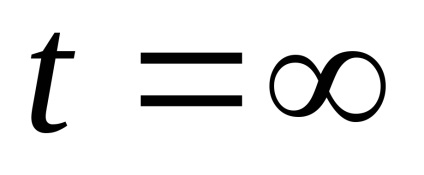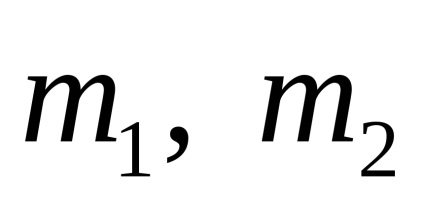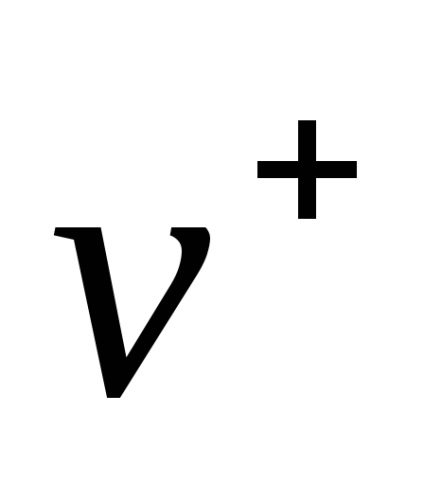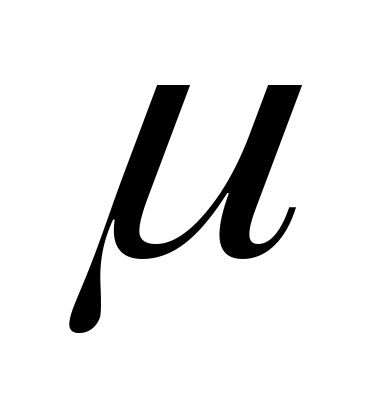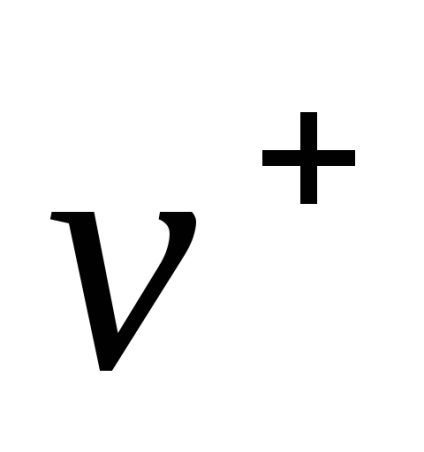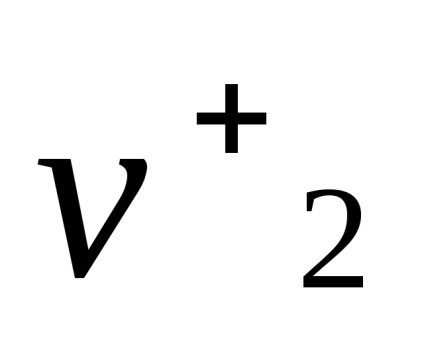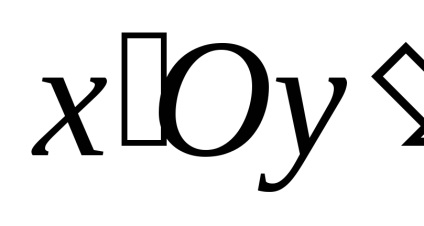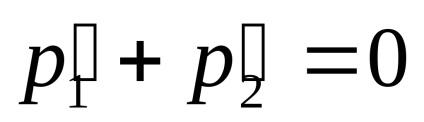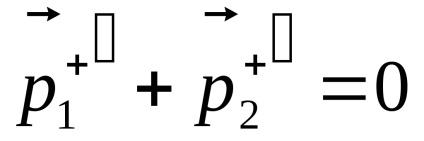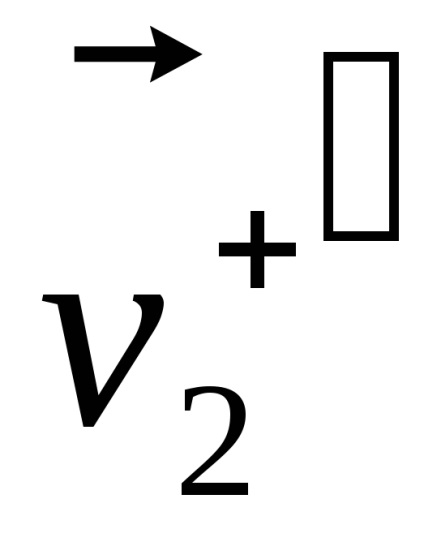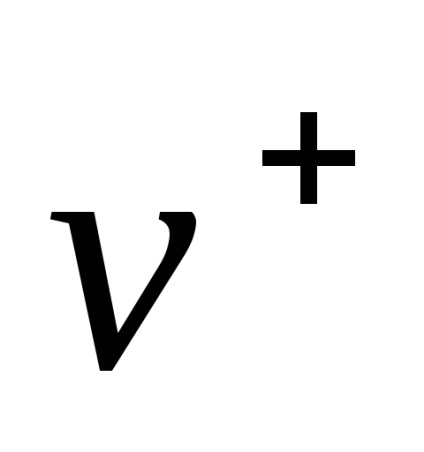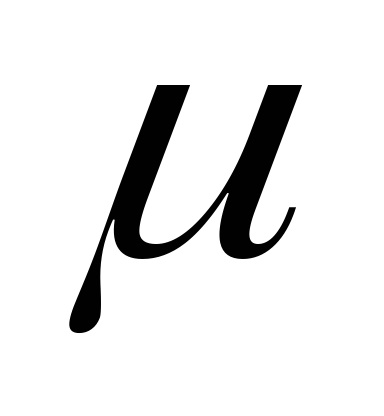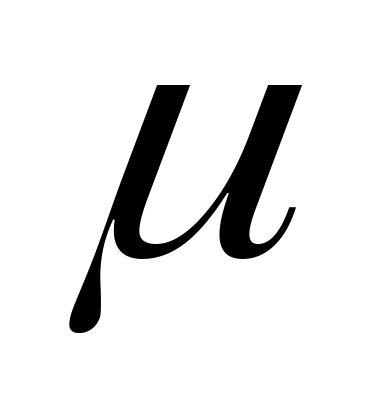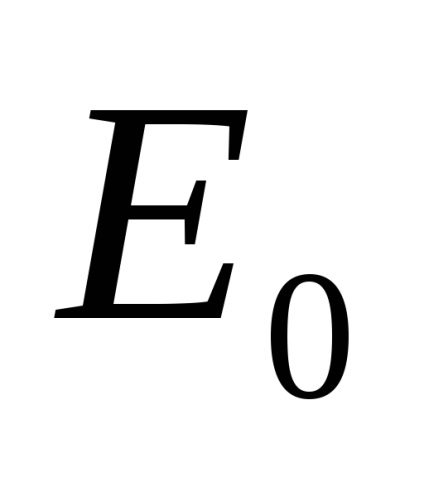6.1. Situația generală a problemei
În mecanică teoretică în cadrul problemei două organisme rezolvate practic două probleme: problema determinării valorilor de energie ale sistemului, traiectoriile particulelor se deplasează într-o regiune limitată de spațiu, iar problema particulelor de dispersie, care include studiul împrăștierii elastice. Două particule de dispersie numit elastic dacă în acest proces nu modifică starea internă a particulelor care interacționează.
Formularea problemei de împrăștiere este după cum urmează. În primul rând, convenabil să-și asume timpul de pornire
. Se presupune că particulele nu interacționează (sunt gratuite), deoarece acestea sunt infinit de departe unul de altul și, prin urmare, energia de interacțiune, este o funcție descrescătoare a distanței dintre ele este zero. Apoi, particulele interacționează unele cu altele, dar când se dispersează pe distanțe lungi și energia lor de interacțiune dispare din nou.
Obiectivul este de a determina starea mecanică a unui sistem de particule cu
, cerându-le să precizeze în . mecanica stări cuantice ale particulelor de la de stat în timpul apelului, în timp ce - Out-state. Este convenabil să urmeze această terminologie și mecanicii teoretice. Este ușor de observat că starea mecanică a unui sistem format din două particule, și Acesta este definit prin viteza lor (sau impulsuri), astfel încât vectorii caracterizează vectori în stare și de stat-Out-Systems. În plus, trebuie să specificați, de asemenea, greutatea particulelor , energia de interacțiune și setarea , Se numește distanța reperare.
Vitezele de particule sunt raportate la un sistem de referință inerțial, care teoretic imprastiere denumit în mod obișnuit sistem de laborator sau n -system. Dacă luăm în considerare problema împrăștierii a celor două fascicule de particule (în acest caz, se presupune că una dintre grinzile de toate particulele au aceeași masă, spun
, și viteza , și în al doilea și apoi, după cum se va vedea mai târziu, trebuie stabilit, de asemenea, unghiul determină orientarea planului de mișcare a fiecărei perechi în raport cu sistemul de referință asociat cu centrul de masă sau o pereche (acest sistem se numește n-sistem).
Două particule de dispersie problemă poate fi rezolvată într-o formă generală, din soluția obținută mai sus problema a două corpuri. De fapt, problema cu două corp vom reduce problema de mișcare
-punct încolo, având în vedere conservarea centrului de masă al vitezei sistemului în procesul de împrăștiere (deoarece sistemul izolat) găsim
unde
- centrul vitezei de masă și viteză -punct după împrăștierea. valoare Noi găsim legea de conservare a energiei pentru -litera (legea de conservare a energiei în cele două organisme în raport cu sistemul c):
Dar din moment ce. prin urmare
, unde , și versorul regia sau .
Procesul de împrăștiere în n sistemul-pot fi reprezentate grafic (fig. 1.6), pe un plan
, care este mișcarea plană a particulelor care interacționează. Să ne amintim că, dacă ca în Fig. 1,6, apoi în conformitate cu (38.5)
,
unde
-Raza - vector -punct.
Deoarece sistemul u S la un moment dat
(Și, prin urmare, și ) Unghiul dintre și egal cu unghiul dintre și și, prin urmare, viteza particulelor în orice punct oppositely regia. Astfel, rezultatul împrăștierii elastice a particulelor este redusă în n vitezele la sistemul-rotație ale celor două particule rămase opuse reciproc și invariabilă în magnitudine. Dar, din moment ce vectorul paralel , Acest unghi este egal cu unghiul de deviere -punct.
Notăm unghiul de deviere a literei
. Vom considera că unghiul polar exprimate în termenii integrala definită:
în cazul în care punctul de cotitură
Este rădăcina ecuației
.
Integrantul în (3.6) conține parametrii care caracterizează
-punct. Este evident că
Aici am folosit o proprietate comună a simetriei calea liniei drepte trasate în centrul terenului cel mai apropiat punct al orbitei. Prin urmare, atât orbita asimptota spun,
-intersecteaza point a spus linie dreaptă la același unghi. unghi numit unghiul de împrăștiere în CMS; este egal cu unghiul dintre cele două asimptote la traiectoria -punct, și - unghiul dintre traiectoria și vectorul asimptota apsidal.
Distanța reperare - distanța dintre asimptote ale traiectoriilor particulelor în n prin care sistemul-particulele trec la împrăștierea. Acesta poate fi, de asemenea, definită ca distanța minimă la care au trecut particulele reciproc în absența interacțiunii dintre ele.
Problema împrăștierea cantităților conservate
și de obicei, scris de viteza și parametrul de impact :
,
Acest lucru arată că din moment
este lungimea perpendiculară a scăzut de la centrul terenului pe traiectoria asimptota -puncte, sau, echivalent, distanța minimă la care -punctul ar trece de la centru, dacă interacțiunea dintre acesta și câmpul ar fi complet absent.
Formulele (1.6) și (4.6) dau soluția problemei difuziei elastică a două particule. Vedem că această problemă este doar un caz special al problemei celor două corpuri, atunci când este necesar să se cunoască doar viteza particulelor după ciocnire la
. unghiul de împrăștiere Depinde numai de , , precum și tipul de interacțiune între particule și parametrii care o caracterizează, adică din