Pentru a rezolva această problemă vom împărți punctele de arc
.
Obținem o linie poligonală înscrisă într-un arc de cerc. Notăm lungimea fiecărui poligon prin link-ul. și prin.
O.2.1. Lungimea curbei este limita la care poligonul inscripționată tinde lungime atunci când lungimea cea mai mare legătură poligon tinde la zero.
Să presupunem că funcția este continuă pe, împreună cu primul său derivat. Și reprezintă. Apoi, în conformitate cu teorema lui Pitagora a unui triunghi dreptunghic cu picioare și de a găsi
.
Folosind teorema lui Lagrange, obținem
.
Lungimea întregii poliliniei. Deoarece funcția este continuă, limita cantitatea integrală obținută există și este egală cu lungimea curbei.
.
Astfel, lungimea arcului curbei într-un sistem de coordonate cartezian este dată de
2.2. Fie funcția definită parametric pe. și anume
. în cazul în care; și. și funcțiile sunt continue și au un prim derivat continuu.
. .
2.3. Fie curba este definită în sistemul de coordonate polare
. . Folosind formulele de trecere de la polare la cartezian sistem de coordonate, obținem:
- curba parametrice. Folosind ecuația (2) găsim
;
.
Apoi, lungimea arcului curbei în coordonate polare este dată de
Acum putem merge pentru a găsi zona de rotație a suprafeței.
suprafață corporală de rotație
Este necesar să se calculeze suprafață corporală formată prin rotirea în jurul axei porțiunii curbe.
Va fi împărțit în părți de puncte. Alăturați-vă punctele care separă corzile. Notăm lungimea fiecărui acord prin
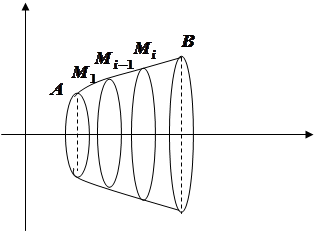
Ca rezultat, rotirea în jurul axei fiecare coardă obține un trunchi de con, a cărei suprafață este egală cu produsul dintre lungimea secțiunii de mijloc circumferențial generatoarei, adică
Este cunoscut faptul că. în cazul în care. prin urmare
Suprafața întregului cifră va fi egală cu
Limita acestei sume (dacă există) și se numește suprafața corpului de rotație.
Cu toate acestea, suma primită nu este o funcție integrantă. dar putem demonstra că limita sumei integrale pentru această funcție va fi egală cu valoarea limită.
Transformarea într-un singur punct
Forma parametrică
În sistemul de coordonate polare