Trapezului klmn flancul KL perpendicular pe bază. Din punctul K pe partea perpendicularei a scăzut MN KA. Pe partea de KL marcat punctul B, astfel încât liniile LA și BN sunt paralele.
a) Demonstrați că BM și MN sunt perpendiculare.
b) Găsiți raportul dintre LA: BN, dacă unghiul este egal cu LMN 150 ^.
a) Pentru a dovedi liniile perpendiculare BM și MN este suficientă pentru a dovedi că BM \ paralel KA, iar acest lucru se face în cazul unor triunghiuri similare SBM și SKA. că este, în cazul în care egalitatea \ Frac = \ frac.
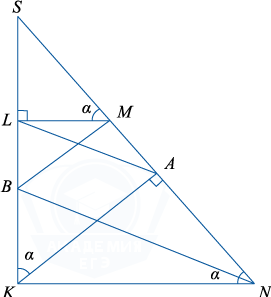
Să SML = \ alpha \ unghi. Apoi \ unghiul SKA = \ unghiul ANK = \ alpha. De linii paralele LA și BN, rezultă că triunghiurile sunt similare cu SLA și SBN, atunci egalitatea \ frac = \ frac.
Într-un triunghi dreptunghic SLM. \ Frac = \ păcat \ alpha. în cazul în care SM = \ frac.
Într-un triunghi dreptunghic SAK. \ Frac = \ păcat \ alpha.
Într-un triunghi dreptunghic SKN. \ Frac = \ păcat \ alpha. SK = SN \ păcatul \ alpha.
Multiplicând ecuație \ \ frac = \ păcat \ alpha = frac \ păcat \ alpha și. obținem: \ frac = \ păcatul ^ 2 \ alfa. SA = SN \ păcatul ^ 2 \ alfa. Având în vedere că \ Frac = \ Frac, am \ Frac = \ păcatul ^ 2 \ alfa. în cazul în care SB = \ frac.
\ Frac = \ frac = \ frac. părțile din dreapta sunt egale, deci \ frac = \ frac, apoi direct LA și BN sunt paralele și perpendiculare pe BM și MN.
b) Având în vedere similitudinea SML și SKN triunghiuri. \ Frac = \ frac.
După cum se arată într-o). \ Frac = \ păcatul ^ 2 \ alfa. Prin ipoteza \ unghiul LMN = 150 ^, \ unghiul LMN + \ alpha = 180 ^, \ alpha = ^ -150 ^ 180 = 30 *.
\ Frac = \ păcatul ^ 2 \ alpha = \ păcatul ^ 30 februarie ^ = \ frac14.
Tipul de locuri de muncă: 16
Subiect: Provocări pentru dovada
Două cercuri cu centrele O_ O_ și, respectiv, se referă la exterior. O_K a avut loc tangentă la cercul al doilea dintr-un punct de O_ (K - punct de contact). și de la punctul O_ O_L a avut loc tangentă la un prim cerc (L - Touch Punct). atinge punctul K și L se află pe părți diferite ale liniei O_O_.
a) Demonstrați că \ unghiul O_KL = \ unghiul O_O_L.
b) Găsiți raza cercului mai mic în cazul în care în plus se știe că este de 4 ori mai mică decât raza cercului mai mare, o zonă de O_KO_L patrulater este de 54 + 9 \ sqrt.
a) Prin proprietatea tangenta la circumferința O_L \ făptașul O_L și O_K \ făptașul O_K. Dreptunghiular \ O_O_K bigtriangleup înscrisă într-un cerc cu diametrul de O_O_.
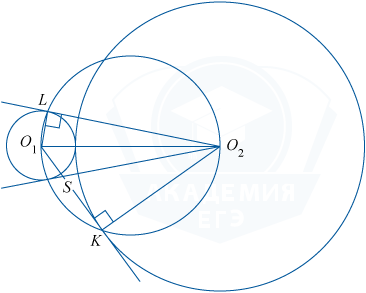
In mod similar, dreptunghiular O_O_L bigtriangleup \ înscrisă într-un cerc cu același diametru. De aceea, \ bigtriangleup O_O_K O_O_L și înscris în același cerc, adică punctul de O_, O_, K. L se află pe un cerc cu diametrul de O_O_. Deci, \ unghiul O_O_L și \ unghiul O_KL - înscris și se bazează pe același arc O_L. Prin urmare, \ unghiul O_KL = \ unghiul O_O_L.
b) Să O_L - raza cercului mai mic. Notăm prin r. În consecință, O_K = 4r. Apoi O_O_ = r + 4r = 5r. Prin urmare, de la \ bigtriangleup O_LO_ pitagoreic O_L = \ sqrt = 2 \ sqrtr. De la \ bigtriangleup O_KO_ pitagoreice O_K = \ sqrt = 3r.
Din condiția rezultă că S_KO_L> = 54 + 9 \ sqrt. Apoi (6+ \ sqrt) r ^ 2 = 54 + 9 \ sqrt (6+ \ sqrt) r ^ 2 = 9 (6+ \ sqrt), r = 3.
Tipul de locuri de muncă: 16
Subiect: Provocări pentru dovada
Două tangent cerc arbitrar unul de altul, sunt scrise într-un unghi predeterminat, valoarea \ alfa. care să nu depășească \ pi.
a) Să se arate că raportul dintre modulul diferenței raze la suma razelor cercurilor este constantă.
b) Găsiți raza cercului mai mic atunci când unghiul \ alpha = \ Frac și raza cercului mai mare este de 10.
a) denota unghi predeterminat prin ABC. Razele cercurilor R_ și R_ (R_ Deoarece centrele cercurilor sunt echidistant față de laturile unghiului, ele se află pe bisectoarea B. Desenați un centru al unui cerc cu raza O_T și O_E la punctul de tangență din partea AB.
Apoi O_T O_E și perpendicular pe AB.
Din centrul cercului mai mic O_ omită perpendicular pe O_K O_E raza mai mare circumferință. Obținem un O_TEK dreptunghi. Apoi EK = TO_ = R_. În consecință, O_K = O_E-KE = R_-R_.
Deoarece O_K \ paralel AB. care \ unghiul ABO _ = \ unghiul KO_O_. Rețineți, de asemenea, că O_O_ = R_ + R_.
Rezultă de aici că \ frac-r _> + r _> = \ fracK> O _> = \ păcatul \ unghiul KO_O_ = \ păcatul \ unghiul ABO_.
Dar \ unghiul ABO _ = \ frac, unde \ alfa - predeterminat unghi, deci \ frac-r _> + r _> = \ păcat \ frac.
b) Substituind valorile dat \ alfa și R_ în formula obținută mai sus, obținem:
Tipul de locuri de muncă: 16
Subiect: Provocări pentru dovada
Trapezul ABCD CD bază perpendicular BC lateral. Prin punctele A și D a avut un cerc care atinge linia BC în punctul M.
a) Demonstrati similaritate \ bigtriangleup ABF și \ bigtriangleup FBK, cu condiția ca F - punctul de trecere a liniilor BC și AD. și BK - înălțimea \ bigtriangleup ABF.
b) Cu condiția CD = 4 cm și AB = 5 cm, se calculează distanța de la punctul M la linia AD.
Fără a pierde din generalitate, putem considera una dintre configurațiile posibile:
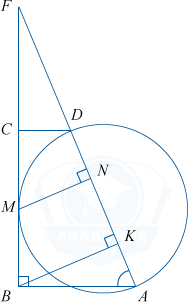
a) Înălțimea \ bigtriangleup ABF \: BK \ făptașul AF \ rightarrow \ bigtriangleup ABF și \ bigtriangleup FBK - dreptunghiulare, ele sunt similare (pentru un unghi larg F).
b) Desenați MN \ AD făptașul. Apoi, MN - distanța de la punctul M la linia AD.
\ Bigtriangleup ABF, \ bigtriangleup MNF, \ bigtriangleup CDF - dreptunghiular, lor unghi ascuțit F - general, astfel încât acestea sunt similare.
\ Bigtriangleup MNF \ sim \ bigtriangleup ABF \ rightarrow \ frac = \ frac, MN = \ frac.
\ Bigtriangleup MNF \ sim \ bigtriangleup DCF \ rightarrow \ frac = \ frac, MN = \ frac.
Prin teorema intersectări și tangentă, avem:
FM ^ = AF \ cdot FD. Apoi, MN ^ = AB \ cdot CD = 20.