Legile de conservare și simetrie a spațiului și timpului.
17.1. Legile de conservare.
Noi am considerat cele trei legi de conservare, de funcționare pentru sistemele închise: legile de conservare a energiei, impuls și momentului cinetic.
In mecanica (in fizica, toate) coordonează, și o funcție de viteză, care rețin mișcare valori constante și depinde numai de condițiile inițiale, numite integralele de mișcare.
Cu toate acestea, nu toate integralele de mișcare în mecanică joacă un rol la fel de important. Printre acestea, există trei. originea, care are o semnificație fizică profundă: ele sunt legate de proprietățile fundamentale ale spațiului și timpului - acestea sunt omogene și izotrope. Toate aceste cantități conservate sunt proprietatea comună importante - aditiv. și anume importanța lor pentru sistemul format din părți, interacțiunea poate fi neglijat (acest lucru nu afectează procesul de deplasare) este suma valorilor pentru fiecare din aceste părți. Această proprietate aditiv ne permite să ia în considerare valorile de joc în mecanica un rol deosebit de important.
afirmație foarte frecvente că legile de conservare este o consecință a omogenității și izotropia de spațiu și timp. Cu toate acestea, ar fi greșit să credem că numai proprietățile specificate de spațiu și timp suficient pentru a lua aceste legi de conservare. Toate aceste legi este o consecință a legilor de mișcare (de exemplu, legea a 2-a lui Newton). Prin urmare, târgul este următoarea declarație:
legi de conservare pot fi derivate din Legea a 2-a lui Newton, atunci când sunt considerate împreună cu proprietățile de simetrie ale spațiului și timpului.
17.2. Simetria de spațiu și timp.
Prin simetria spațiului și timpului, înțelegem omogenitatea spațiului și timpului, precum și spațiul izotrop. Care este omogenitatea de timp, spațiu și izotropia spațiu? Noi explica ce este sensul investit în aceste concepte.
1) timp de Uniformitatea înseamnă că, în cazul în care oricare două puncte în timp toate corpurile sistemului închis pus în exact aceleași condiții, dar pornind de la aceste momente, toate fenomenele din acest sistem va proceda în același mod.
2) Uniformitatea spațiu înseamnă că, în cazul în care un sistem închis de organisme să se mute dintr-un loc în spațiu în altul, supunerea tuturor organismelor din ea în aceleași condiții în care acestea au fost în aceeași poziție, aceasta nu afectează cursul evenimentelor ulterioare.
3) spațiu izotropă înseamnă că, în cazul în care un sistem închis de corpuri în spațiu se rotesc la orice unghi, în timp ce pune toate corpurile în ea în aceleași condiții în care acestea au fost în aceeași poziție, nu afectează cursul evenimentelor ulterioare.
Aceste proprietăți ale spațiului și timpului - generalizarea fundamentală a faptelor experimentale.
17.3. Omogenitatea spațiului, și legea conservării impulsului.
Deci, datorită omogenității proprietăților mecanice ale unui sistem închis nu este schimbat în nici un sistem de transport în paralel ca un întreg în spațiu.
Se transferă sistemul dintr-o poziție arbitrară
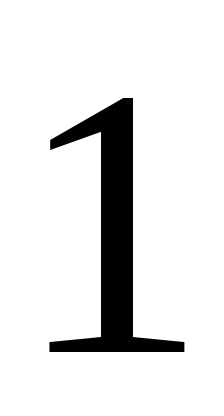
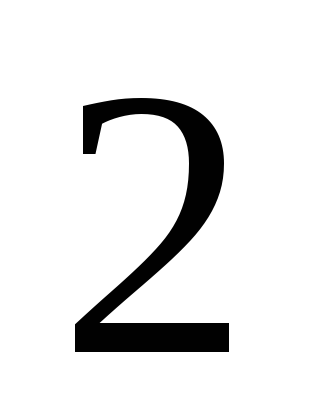
Utilizarea într-un sistem închis de putere
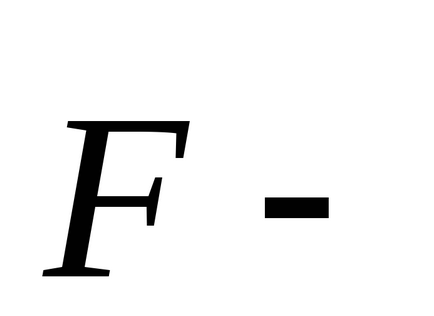
Deoarece spațiul este uniformă, atunci când transferul tuturor particulelor din sistem în spațiu, la aceeași distanță
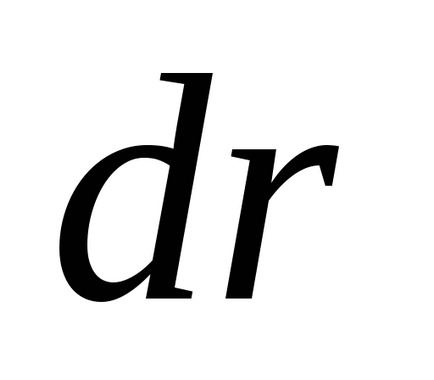
pentru orice
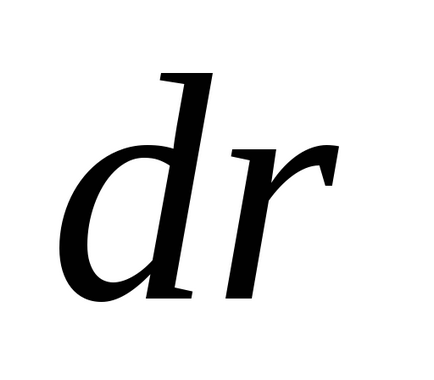
.
Apoi, a doua lege a lui Newton de conservare a impulsului obținem:
Din discuția de mai sus, este un alt rezultat important.
Având în vedere că suma tuturor forțelor care acționează într-un sistem închis este zero, atunci putem scrie
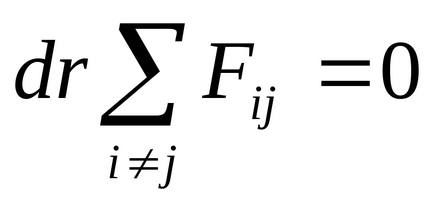
unde
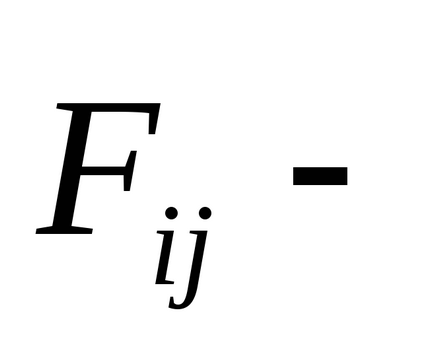
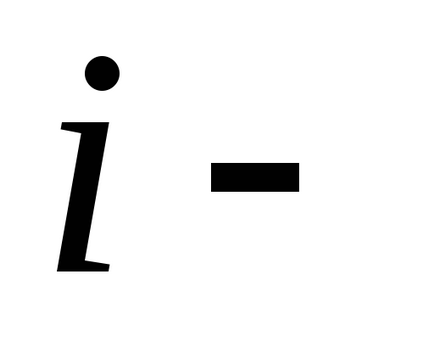
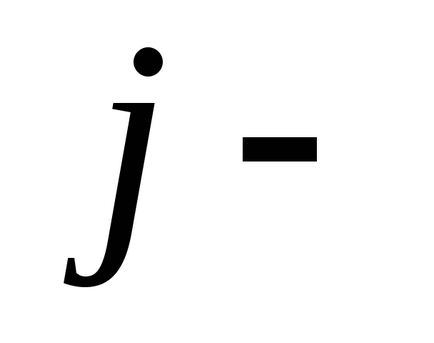
Rescrierea această condiție în mod diferit
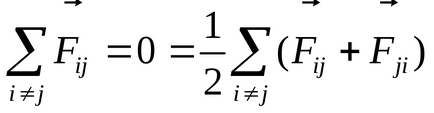
având în vedere independența fiecăreia dintre interacțiunea perechilor de particule unul cu celălalt vom obține a treia lege a lui Newton:
Pentru un sistem închis legea conservării impulsului rezultă în mod oficial din două legea Newton, dacă presupunem că toate forțele care acționează sunt supuse legii forțelor de acțiune și de reacție (a treia lege a lui Newton).
Cu toate acestea, punerea în aplicare a treia lege a lui Newton, precum și legea conservării impulsului, spațiu obuslovlenyodnorodnostyu.
Notă. În cazul în care operatorii de transport de impulsuri nu sunt doar un corp material, dar, de asemenea, domeniul, a treia lege a lui Newton în această formulare nu este aplicabilă.
În același timp, ținând seama de contribuția câmpului, pentru un sistem închis de corpuri de omogenitatea spațiului, vom obține din nou legea de conservare a impulsului:
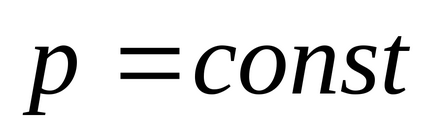
17.4. Izotropia spațiului și legea conservării momentului cinetic.
Izotropia spațiului înseamnă că, la rotirea sistemului închis la orice unghi în spațiu în cadrul acestui sistem nu va fi nici o schimbare.
Pentru un sistem închis de corpuri de cupluri de externe
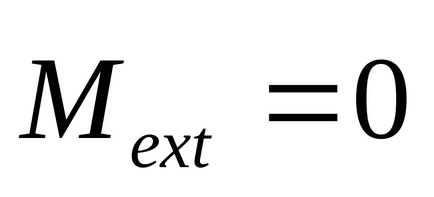
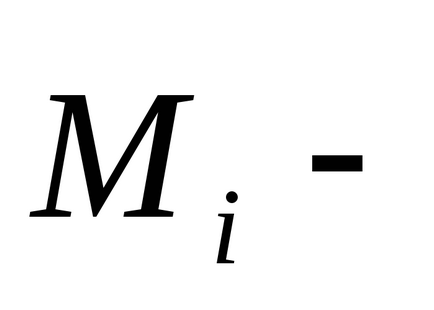
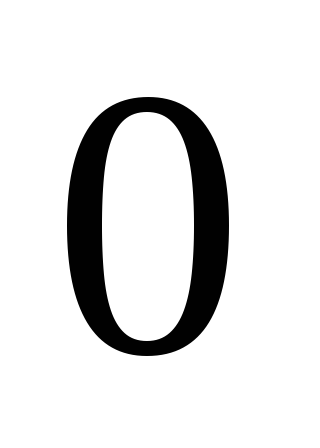
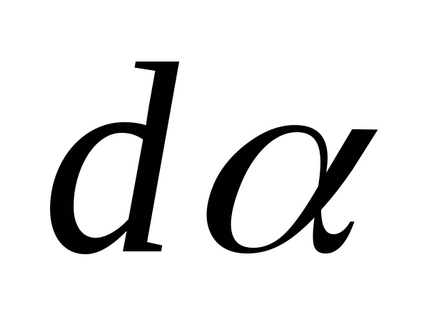
spațiu izotropie Datorită în cadrul sistemului de nici o schimbare în această inversare nu are loc, adică, forța de muncă care funcționează în cadrul sistemului ar trebui să fie zero:
.
Având în vedere arbitrarietatea unghiului
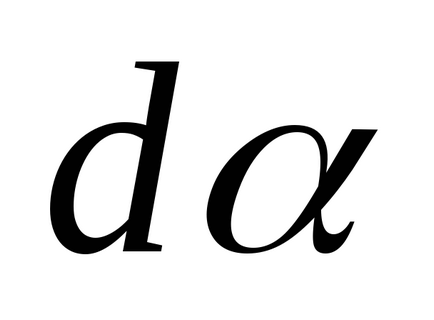
Și urmează legea conservării momentului cinetic:
17.5. Legea conservării energiei și omogenitatea timpului.
Având în vedere problemele de dinamică, avem rezultatul a două legi a lui Newton - forța de muncă, efectuat asupra sistemului mecanic, este egală cu creșterea energiei cinetice:
Vom mai întâi considerare în legătură cu un punct al materialului.
divulga
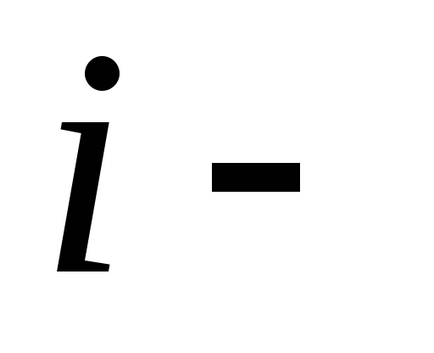
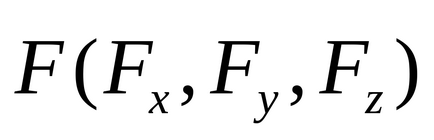
In cazul cel mai general energia potențială (de exemplu, pentru un sistem deschis) poate depinde nu numai pe coordonatele, dar încă la timp: incrementarea totală și potențialul funcției include, de asemenea, un derivat de timp (adică diferențial introducerii complete 4 variabile ):
La sfârșitul poziției punctului de material în mișcare
Pentru un sistem închis de corpuri privind activitatea forțelor care se misca de integrala
adăugați și scade partea din dreapta a derivatului parțial în raport cu timpul, atunci
Rezumând asupra tuturor punctelor materiale ale sistemului, vom obține lucrarea de egalitate
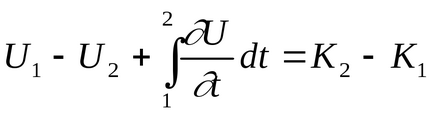
Acest rezultat este, de asemenea, valabil pentru sisteme deschise.
Referindu-ne din nou la sistemul închis de organisme și de a folosi proprietatea de omogenitate a timpului.
Uniformitatea timpului este că, pornind de la orice punct în timp de evenimente trebuie să aibă loc în același mod, și anume, timp energia potențială a sistemului închis de corpuri (puncte de masă), omogenitatea nu poate depinde în mod explicit la timp
De unde legea de conservare a energiei:
În loc de concluzie. între ecuațiile dinamice și legile de conservare este o diferență esențială.
Legile dinamica ne oferă o imagine detaliată a procesului. Legile de conservare sunt cauzate de proprietățile fundamentale ale spațiului și timpului, și astfel încât acestea sunt universale și cuprinzătoare. Dar ele nu oferă orientări detaliate cu privire la progresul unui proces. Ei vorbesc doar despre ce procese sunt interzise în natură. Legile de conservare acționează ca restricții (limite)! Dacă, de exemplu, se pare că unele proces este contrar legilor de conservare, este imediat posibil să se afirme că acest proces este imposibil și lipsit de sens să încerce să-l pună în aplicare.