Astăzi, vom merge la următorul nivel de calificare în găsirea derivata - studiu derivatului logaritmică și funcția de putere exponențială derivat. Citind acest tutorial presupune că știți deja cum să găsească derivata funcții simple și complexe, sume acestora, produse și relații. Dacă ceva din cele de mai sus este cauza problemele, atunci ar trebui să exploreze tema „Cum de a găsi derivat“ și „derivat al unei funcții compozit.“ Presupunem că aceste subiecte ați trecut deja.
Luați în considerare acest exemplu:
Exemplul 1. Găsiți derivata funcției
soluţie:
Există mai multe opțiuni pentru a găsi derivata acestei funcții. Primul - este „cap“. Ie vopsea pentru a începe derivat privat, lucrări derivate și apoi ia în considerare, ia, ia ... Dezavantajul acestei metode constă în faptul că, în procesul de soluții se va întinde fracțiuni foarte greoaie, care pe scurt confuz și să facă greșeli.
A doua opțiune - pentru a încerca să convertească funcția derivat (simplificată). În cazul nostru, ar fi frumos dacă pentru a găsi derivat al unui produs sau pur și simplu stânga sau doar atitudinea. Pentru a face acest lucru, eliminați paranteze în numărătorul, de ieșire vom obține o fracție, în care atât numărătorul cât și numitorul polinoame. Diferentiaza astfel de fracțiune va fi deja mai ușor.
A doua cale este sarcina rezolvata ....
Și, în sfârșit, a treia, și cea mai simplă opțiune - pentru a rezolva această sarcină cu ajutorul derivatului logaritmică. De ce ai nevoie? Toate simplu banal: trebuie să „stea“ logaritmii pe ambele părți ale ecuației.
Acum trebuie să ne amintim proprietățile logaritm, și anume că logaritmul produsului este suma logaritmilor, iar logaritmul raportului este egală cu diferența dintre logaritmii, adică
Și vom avea nevoie de o altă proprietate utilă a logaritmului: gradul de logarithm poate fi scos din ea
Acum, se aplică aceste proprietăți pentru funcția noastră
Rămâne să se diferențieze. Sper că vă amintiți ce este derivata logaritmului - în cazul în care nu se vedea imediat derivat tabelul sau descărcați-l pe computer.
Diferențierea partea dreapta nu ar trebui să provoace dificultăți, și acești derivați, am găsit mai mult decât o dată. Dar, pe partea stângă este în valoare de a spune câteva cuvinte. Doar scrie că - nu este suficient, pentru că - este o funcție complexă care depinde. Prin urmare, derivatul trebuie considerat ca un complex de funcții, și anume .
obține
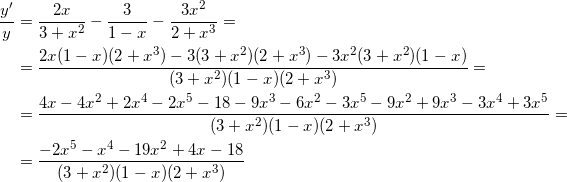
Ie ne-am format, rămâne doar să-și exprime, se deplasează în partea dreaptă
Înlocuim valoarea condiției și transformare, în cazul în care convertiți
Diferențierea folosind logaritmi este comod de utilizat atunci când este administrat la un nivel de expresie sau de exprimare greoaie. În primul caz, logaritmii ajută să rupă expresia în componente mai mici, în al doilea - pentru a scăpa de gradul.
Să vedem un alt exemplu
Exemplul 2. Găsiți derivata funcției
soluţie:
logaritmi „Hang“
Aplicarea proprietăților logaritmi
Un caz particular este gradul de funcții de putere exponențială. Ele sunt în sol și în măsura în care a găsit. Cel mai simplu exemplu de o funcție exponențială de putere
Exemplul 3. Găsiți derivata funcției
soluţie:
Noi folosim metoda de diferențiere logaritmice
Aplicarea proprietăților de logaritmi pentru gradul
Dar, în practică, de regulă, există mai multe funcții complexe de putere exponențială.
Exemplul 4. Găsiți derivatul
soluţie:
logaritmi Stai pe ambele părți
Aplicați proprietatea logaritmului