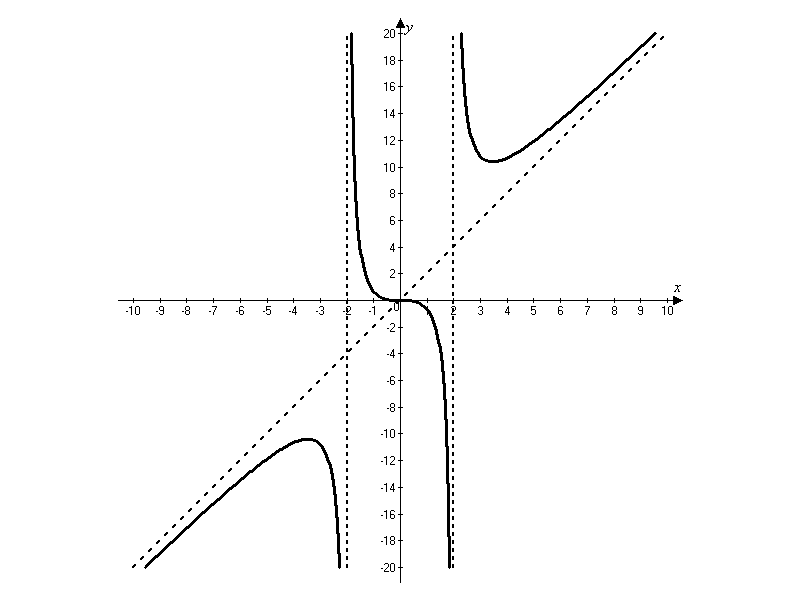
Referințe: [3], Ch. V, § 10
numita asimptotă directă a curbei y = f (x), în cazul în care distanța de la punctul M la curba linie dreaptă tinde la zero, ca punctul M de-a lungul curbei la infinit de origine (fig. 1.7).
Distinge între asimptotă verticală și oblică. Asimptota verticală are o ecuație de forma x = x0, și este o linie paralelă cu axa Oy. Ecuația asimptotă Înclinat are forma y = kx + b. În cazul particular al k = 0 se numește asimptota orizontală, ca ecuația y = ei b este o linie paralelă cu Ox.
Să o y = curba f (x). Pentru a găsi asimptota verticală a punctelor de curbă sunt infinite ruptură sale (puncte de pauză de al doilea tip).
apoi linia dreaptă x = x0 ─ asimptota verticală a curbei y = f (x) (Fig. 1.8).
asimptotă Înclinat și orizontală.
Să presupunem că o curbă y = f (x). Pentru a găsi asymptotes înclinate ecuație y = kx + b, sunt coeficienții k și b. calcularea limitelor:
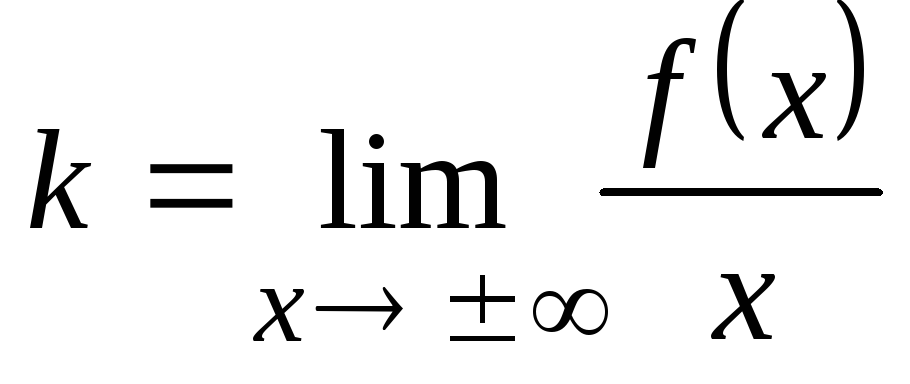
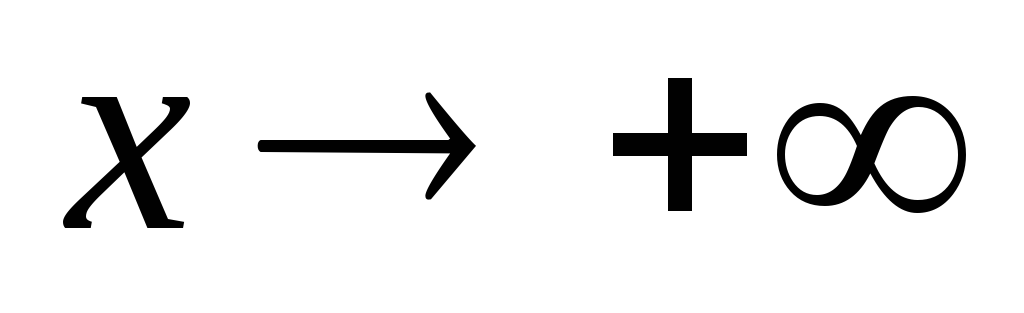
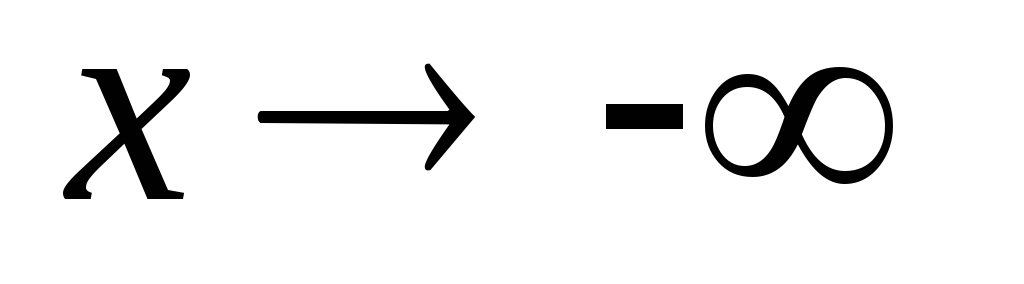
În cazul special în care k = 0 și b ─ număr finit, curba are o asimptotă orizontală a cărei ecuație y = b.
Exemplu. Găsiți asimptota curbei
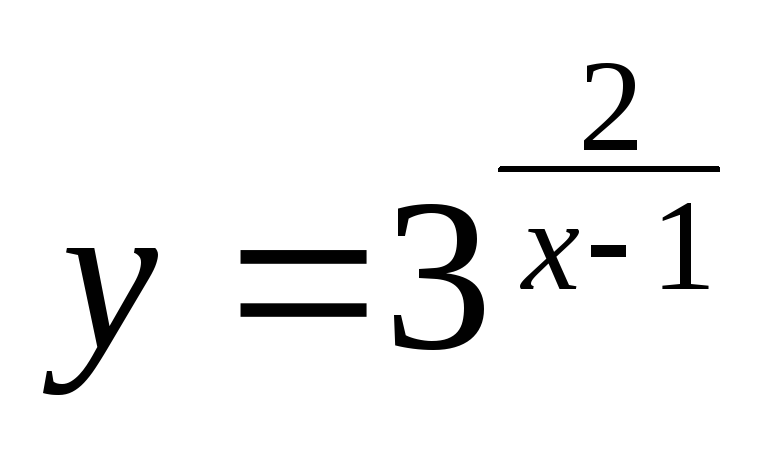
Decizie. funcție
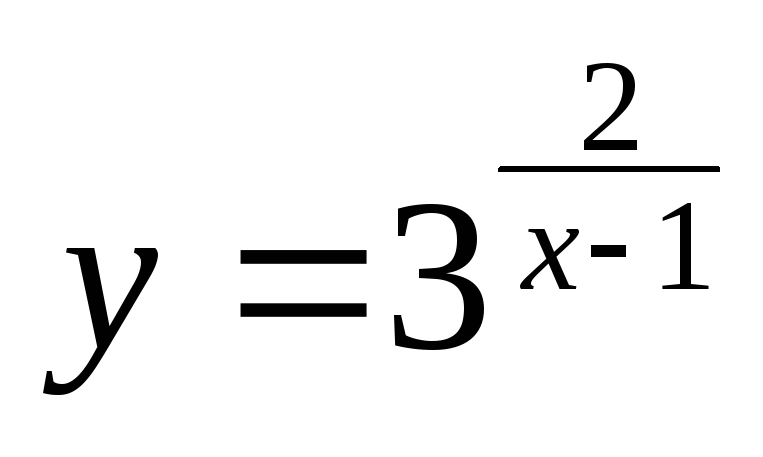
,
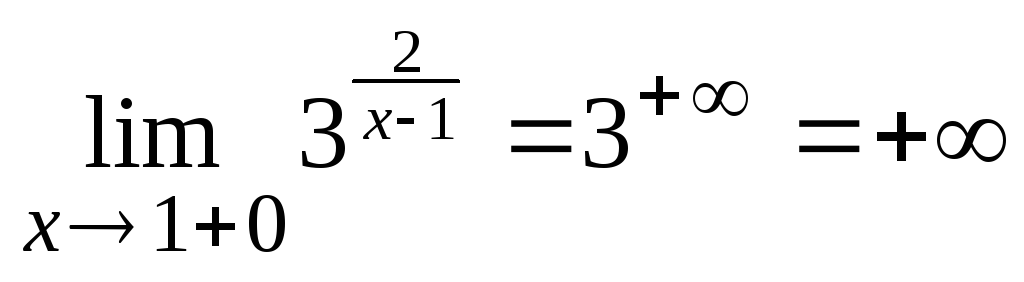
Deoarece una dintre limitele este infinit, x = 1, este un punct de discontinuitate al doilea tip, și prin urmare, curba are o asimptotă verticală x = 1.
Determina dacă curba asimptota orizontale sau înclinate. Pentru a face acest lucru, vom calcula limitele corespunzătoare:
, Ecuația asimptotyy = kx + b ia forma y = 1 (asimptotă orizontală).
Grafic hematichesky funcției prezentate în Fig. 1.9.
1.14. Conducerea unei investigații complete a funcției și construcția a graficului său
Referințe: [3], Ch. V, § 11
1. Găsiți domeniul funcției.
2. Setați funcția de paritate impar, periodicitate. Găsim punctele caracteristice, cum ar fi punctul de intersecție cu axele de coordonate.
3. Găsiți punctul de discontinuitate a funcției, definim caracterul lor. Dacă un al doilea tip de puncte de pauză (puncte de discontinuitate a infinit) disponibilitatea set Graficul de asymptotes verticale.
4. Găsiți derivata funcției, punctele critice, intervalele de monotonie, punctul extremelor și valoarea funcției la aceste puncte.
5. Găsiți derivata a doua a funcției, intervalele de convexitate și concavitatea curbei și punctul de inflexiune al graficului funcției.
6. Setați prezența curbei investigate înclinat și asymptotes orizontale.
7. Din datele obținute graficul de construcție.
Notă. Dacă o funcție este par sau impar, studiul este realizat nu pe întreaga axă reală și în intervalul [0, + ∞). Apoi continuați graficul simetric față de ordonata la intervalul (-∞, 0) în cazul în care o funcție chiar și în raport cu centrul sistemului de coordonate, în cazul în care o funcție impar.
Dacă funcția este periodică, graficul acesteia construit pentru o perioadă, și apoi să continue să periodic întreaga axă.
Exemplu. Pentru a efectua un studiu complet al funcției
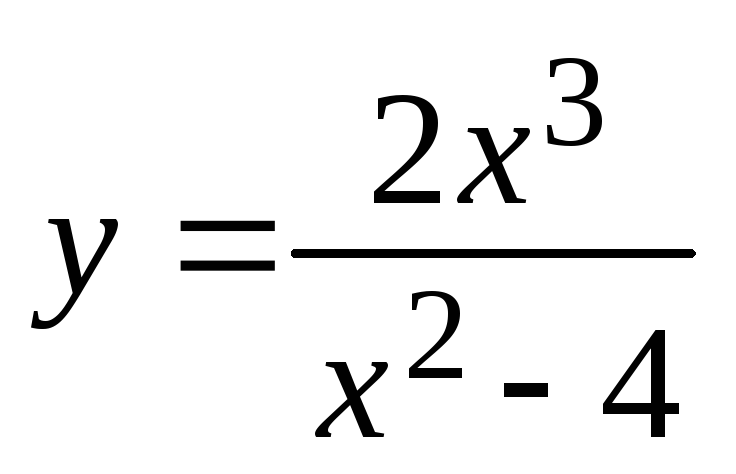
1. Funcția definită și continuă pe axa întregii reale exceptând punctele x = ± 2.
2. Funcția este ciudat, ca o condiție pentru ea. Prin urmare, este suficient să se realizeze un studiu privind intervalul [0, + ∞).
3. În intervalul [0, + ∞) are un punct de pauză x = 2. investiga natura punctelor de pauză, care calculează următoarele limite:
,
Deoarece limitele unilaterale sunt nelimitate, linia x = 2 este o asimptotă verticală.
4. Găsiți primul derivat:
.
Noi găsim punctele critice pe intervalul [0, + ∞):
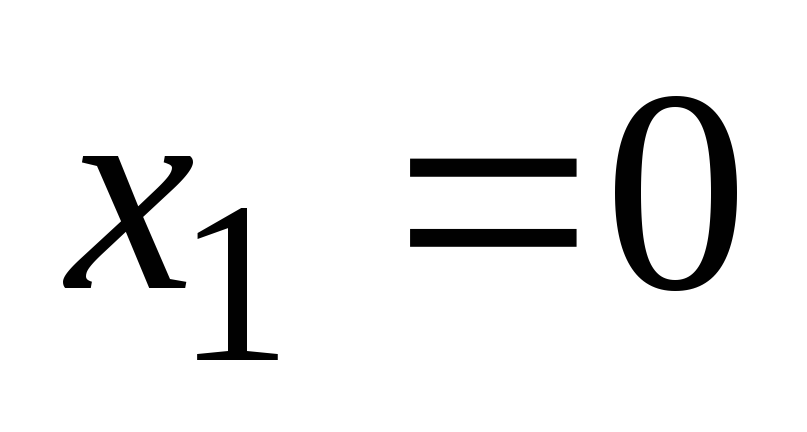
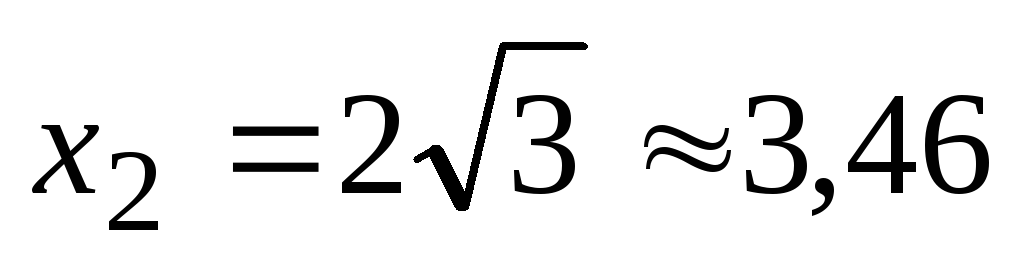
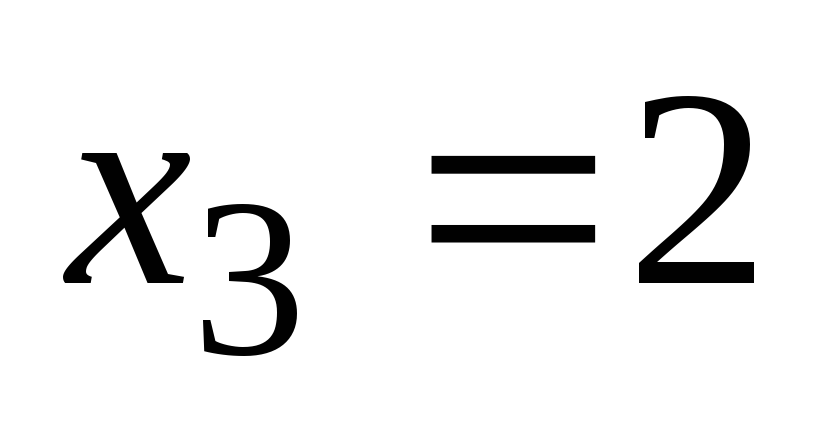
5. Găsiți derivata a doua:
.
Derivata a doua pe intervalul [0, + ∞) devine zero la punctul x1 = 0 și este la punctul x3 = 2, care nu este inclusă în domeniul funcției.
Datele obținute sunt construirea unui tabel:
În primul rând al tabelului intervalelor specificate pentru care punctul critic și punctul în care derivata a doua este egal cu zero sau nu există, se împarte intervalul [0, + ∞). A doua linie arată semnul primul derivat al acestor intervale, iar al treilea - un semn al doilea derivat. A patra linie prezintă arbitrar majorarea sau reducerea funcției pe intervalul (în funcție de semnul primei derivate), iar convexitatea sau concavitatea curbei (semnul derivatei a doua).
6. Cautam asimptota oblică:
,
.
Curba în intervalul [0, + ∞) are o asimptotă înclinată
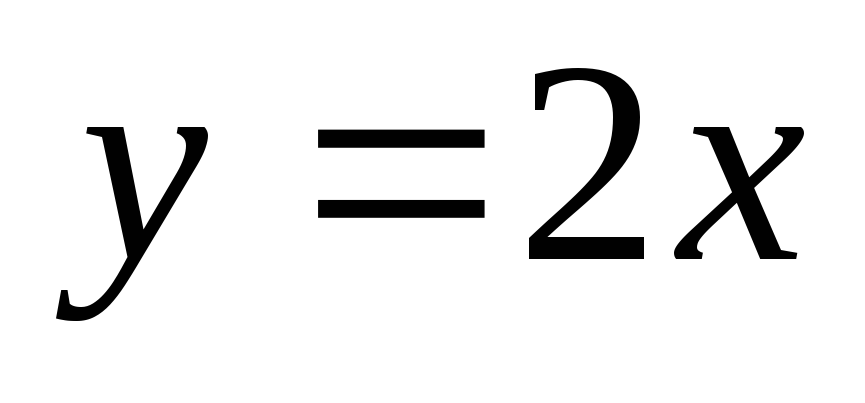
Construirea verticale x = 2 și y = 2x asymptotes înclinate, iar apoi datele din tabelul construi un grafic al funcției pe intervalul [0, + ∞), care poate continua apoi la intervalul (-∞, 0) este simetrică față de centrul sistemului de coordonate.