Proprietățile produsului vectorial
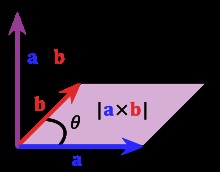
Suprafața unui paralelogram este egală cu produsul vectorial
- Vectori a și b> coliniari dacă și numai dacă a x b = 0 = \ mathbf>. Din definiția rezultă că dispariția produsului cruce este echivalentă sau egalitatea cu zero a unuia dintre factorii (un vector de zero este coliniar cu restul) sau dispariție sinusul unghiului dintre vectori. Deoarece orice coliniare vector pentru sine, apoi a × a = 0>.
- Modul produs vector numeric egală cu aria paralelogramului formate pe acești vectori. Acest lucru rezultă din definiția. Să e> - versorul perpendicular pe vectorii a și b> și selectați astfel încât triplu (ab e), \ mathbf)> orientat pozitiv, S Π (a b)) >> -. Zona paralelogramului construit pe vectorii a și b>. Apoi a x b = S Π (a. B) e = S _)> \ mathbf>.
- Anticommutativity: a x b = - b × a = - \ mathbf \ ori \ mathbf>.
- Asociativitatea multiplicare relativ scalar: (k a) x b = k (a x b) = a x (k b) = k (\ mathbf \ ori \ mathbf) = \ mathbf \ ori (k \ mathbf)>.
- Distributivitatea prin adăugarea: (a 1 + a 2) x b = 1 × b + a 2 x b + \ mathbf _) \ ori \ mathbf = \ mathbf _ \ ori \ mathbf + \ mathbf _ \ ori \ mathbf>.
- Identitatea Jacobi: (a × b) × c + (b × c) × a + (c × a) × b = 0) \ ori \ mathbf + (\ mathbf \ ori \ mathbf) \ ori \ mathbf + (\ mathbf \ ori \ mathbf) \ ori \ mathbf = \ mathbf>.
- identitate Lagrange: a × (b × c) = b (a ⋅ c) - c (a ⋅ b) \ ori \ mathbf) = \ mathbf (\ mathbf \ cdot \ mathbf) - \ mathbf (\ mathbf \ cdot \ mathbf )>. Pentru a memora utilizarea mnemotehnică „BAC minus TSAB»
Vector produs într-un sistem de coordonate ortonormală Editare
a x b = (a 1 e 1 + a 2 e 2 + 3 e 3) × (b 1 e 1 + b 2 e 2 + b 3 e 3) = = a 1 b 1 e 1 × e 1 + un 2 b 2 e 2 × e 2 + 3 b 3 e 3 x e 3 ⏟ 0 + (a 1 b 2 - a 2 b 1) e 1 × e 2 ⏟ e 3 + (a 1 b 3 - a 3 b 1) e 1 × e 3 ⏟ - e 2 + (a 2 b 3 - a 3 b 2) e 2 x e 1 3 ⏟ e = = | un 2 a 3 b 2 b 3 | e 1 - | 1 a 3 b 1 b 3 | e 2 + | a 1 a 2 b 1 b 2 | e = 3 | un 2 a 3 b 2 b 3 | e 1 + | a 3 a 3 b 1 b 1 | e 2 + | a 1 a 2 b 1 b 2 | e 3 \ mathbf \ ori \ mathbf = (A_ \ mathbf _ + a_ \ mathbf _ + a_ \ mathbf _) \ ori (B_ \ mathbf _ + B_ \ mathbf _ + B_ \ mathbf _) = \\ = \ underbrace B_ \ mathbf _ \ ori \ mathbf _ + a_b_ \ mathbf _ \ ori \ mathbf _ + a_b_ \ mathbf _ \ ori \ mathbf _> _> + (a_b_-a_b _) \ underbrace _ \ ori \ mathbf _> _ _> + (a_b_-a_b _) \ underbrace _ \ ori \ mathbf _> _ _> + (a_b_-a_b _) \ underbrace _ \ ori \ mathbf _> _ _> = \\ = a_a _ \\ b_b_ \ end> \ mathbf _ a_a _ \\ b_b_ \ end> \ mathbf _ + _ a_a \\ b_b_ \ end> \ mathbf _ = _ a_a \\ b_b_ \ end> \ mathbf _ + _ a_a \\ b_b_ \ end> \ mathbf _ + _ a_a \\ b_b_ \ end> \ mathbf _ \ end >>