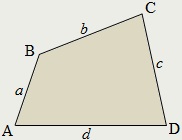
Patrulater numit figura, care este format din patru puncte (vârfuri) și patru segmente (părți) care conectează secvențial sus. În acest caz, nici unul dintre cele trei puncte de date nu se află pe aceeași linie dreaptă, și conectarea segmentele lor nu trebuie să se suprapună.
De patrulater este convexă în cazul în care este situat într-o jumătate de plan în raport cu linia care conține oricare dintre părți.
Suma unghiurilor unui patrulater convex este de 360 °:
Nu există nici un quad-uri, toate unghiurile a căror sunt toate unghiurile obtuze sau acute.
Fiecare colț al patrulaterului este întotdeauna mai mică decât suma celorlalte trei unghiuri:
∠A <∠B+∠C+∠D. ∠B <∠A+∠C+∠D.
∠C <∠A+∠B+∠D. ∠ D <∠A+∠B+∠D .
Fiecare parte a patrulaterului este întotdeauna mai mică decât suma celorlalte trei laturi:
Suprafața unui patrulater convex arbitrar este egal cu:
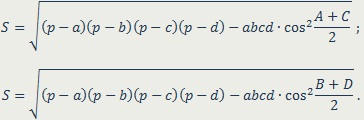
Diagonalele patrulaterului sunt numite segmente care leagă vârful său opus.
Diagonalele unui patrulater convex se intersectează, și un non-convexe - nr.
Zona arbitrară patrulater convex:
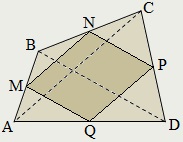
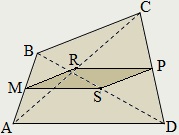
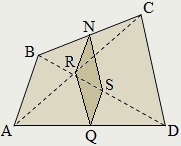
Dacă M. N. P. Q - ale punctelor mediane laturile unui patrulater convex ABCD. și R. S - mijlocul diagonalele, dreptunghiuri MNPQ. MRPs. NSQR sunt paralelograme și Pierre Varignon numit paralelogram.
Forma și mărimea paralelograme Pierre Varignon referitoare la forma și mărimea ABCD patrulater. Deci, MNPQ - un dreptunghi, în cazul în care diagonalele ABCD patrulater sunt perpendiculare; MNPQ - diamant, în cazul în care diagonalele ABCD patrulater sunt egale; MNPQ - box în cazul diagonalelor ABCD patrulater sunt perpendiculare și egale;
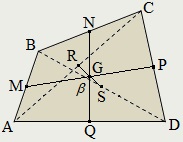
Segmente MP. NQ și RS sunt numite primul, al doilea și al treilea centru de linii ale unui patrulater convex.
Într-un paralelogram, și numai în ea, mijlocul diagonalele sunt aceleași, și, prin urmare, a treia linie de centru degenerează într-un punct. Pentru alte patrulatere de linia de mijloc - segmente.
Toate patrulater linie secundară se intersectează la un moment dat și împărțiți-l în jumătate:
Suma pătratelor linia medie a patrulaterului este un sfert din suma pătratelor toate laturile și diagonalele sale:
MP 2 + NQ 2 + 2 RS = ¼ (AB + BC 2 2 2 + CD + AD 2 + AC 2 + BD 2).
Dacă β - unghiul dintre primul și al doilea liniile mediane ale patrulaterului, aria suprafeței:
SABCD = MP · NQ · β păcat.
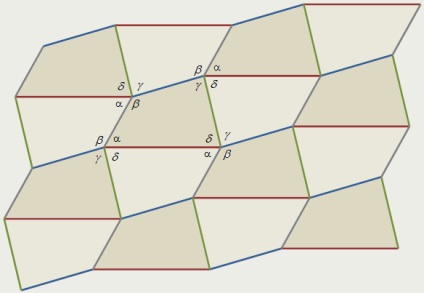

Egalitatea de plăci care au o formă arbitrară, nu este convexă în mod necesar, capacul patrulater un plan, astfel încât nu există nici o suprapunere de inele pe partea de sus a reciproc și porțiunile neacoperite au rămas plan.
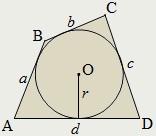
De patrulater numit descris în jurul circumferinței (așa cum este descris), în cazul în care există un cerc care atinge toate laturile sale, în timp ce cercul înscris în sine este numit.
Este descrisă patrulater dacă și numai dacă, cantitatea de cod din laturile sale opuse sunt egale:
Pentru laturile patrulatere descrise și raza unui cerc înscris în ea fidel:
Descris zona patrulater:
unde r - raza cercului inscris, p - patrulater semiperimetrul.
Descris zona patrulater:
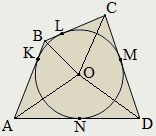
Centrul cercului înscris în patrulaterul este un punct de intersecție a Bisectoarele cele patru colțuri ale patrulaterului.
Punctul de tangență al cercului inscris se taie segmente egale pe unghiurile unui patrulater:
AK = AN. BK = BL. CL = CM. DM = DN.
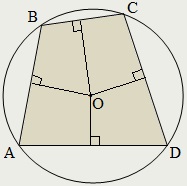
Dacă O - centrul unui cerc înscris într-un pătrat pe ABCD, atunci
∠AOB + ∠COD = ∠BOC + ∠AOD = 180 °.
Pentru ABCD patrulater descrisă cu laturile AB = a. BC = b. CD = c și d = AD relații adevărate:
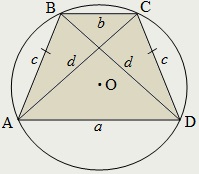
Patrulatera numit un cerc înscris (înscrise) în cazul în care există un cerc care trece prin vertexului, atunci cercul în sine este numit descris aproximativ patrulateră.
Patrulaterul convex este descrisă, și apoi numai atunci când suma unghiurilor opuse este egal cu 180 °:
∠A + ∠C = ∠B + ∠D = 180 °.
Centrul descris despre circumferința patrulaterului este un punct de intersecție dintre toate cele patru laturi ale midperpendiculars acestui patrulater.
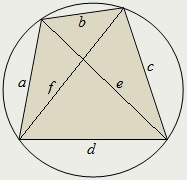
Prima teorema lui Ptolemeu. Convex patrulater dacă și numai dacă se înscrie, în cazul în care egalitatea:
A doua teorema lui Ptolemeu. Convex patrulater dacă și numai dacă se înscrie, în cazul în care egalitatea:
Raza cercului circumscris despre patrulater:
Zona patrulater înscris:
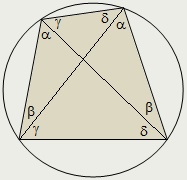
Diagonală divide patrulater convex fiecare unghi de pe cele două colțuri. Corners, sprijinindu-se într-o parte, a spus să fie legate colțuri.
patrulater convex este înscrisă dacă și numai dacă are cel puțin o pereche de unghiuri egale legate.
Am înscris patrulater oricare două unghiuri înrudite sunt egale.
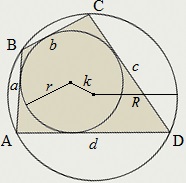
În cazul în care patrulaterul este atât descrisă și înscris, zona sa:
Razele cercurilor circumscrise și inscripționate patrulaterului și distanța dintre centrele cercurilor este relația:
Paralelogramul numit patrulater, laturile opuse ale care sunt paralele:
La laturile opuse ale unui paralelogram sunt egale și unghiurile opuse sunt egale:
∠A = ∠C. ∠B = ∠D.
Suma oricăror două unghiuri adiacente paralelogram este egală cu 180 °:
∠A + ∠ B = ∠ B + ∠ C = ∠ C + ∠ D = ∠ A + ∠ D = 180 °.
diagonalele de paralelogram se intersectează și punctul de intersecție sunt împărțite în jumătate:
Fiecare diagonală împarte paralelogramul în două triunghiuri egale:
∠ ABC = ∠ CDA; ∠ ABD = ∠ CDB.
Două diagonalele unui paralelogram se împarte în patru egal-triunghi:
Suma pătratelor diagonalele unui paralelogram este egală cu suma pătratelor toate laturile sale:
e 2 + f 2 = a 2 + b 2 + a 2 2 + b 2 = (a 2 + b 2).
- În cazul în care un patrulater laturile opuse sunt egale, atunci patrulaterul - un paralelogram.
- Dacă un patrulater cele două părți opuse sunt egale și paralele, atunci patrulaterul - un paralelogram.
- Patrulater, care în diagonală, la un punct de intersecție împărțită în jumătate - un paralelogram.
- Dacă unghiurile opuse ale unui patrulater sunt egale, atunci patrulaterul - un paralelogram.
Înălțimea paralelogramului se numește perpendicular realizat de sus a paralelogramului de partea neprilezhaschey:
Suprafața unui paralelogram poate fi determinată:
- prin direcția și înălțimea lui, conected să-l:
- prin două dintre laturile sale și un unghi între ele:
S = ab · γ sin.
Trapez numit patrulater ale cărui doar două laturi opuse sunt paralele:
laturile paralele sunt numite baze ale trapezoidală, non-paralela - flancurilor.
Înălțimea trapezului - realizată perpendicular cu un punct arbitrar al unei baze trapezului la o linie care conține o bază diferită de trapez.
Linia de mijloc (prima linie de mijloc) se numește segment de trapez, care face legătura între punctele mediane ale părților laterale ale trapezului:
Linia mediană a trapezului este paralela cu baza sa, și este egală cu jumătate din suma dintre:
KL = ½ (AD + BC).
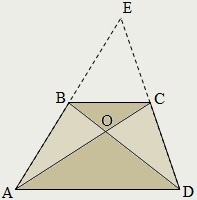
Cu continuat până se intersectează laturile trapezului formează două triunghiuri similare cu factorul de similaritate egal cu bazele raportului:
δ AED ∼ δ BEC. k = AD / BC.
Triunghiurile formate de principiile și segmentele diagonale cu factor de similaritate egal cu bazele raportului:
δ OCD ∼ δ COV. k = AD / BC.
Zonele de triunghiuri formate de laturile și diagonalele segmente trapezoizi sunt egale:
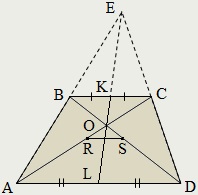
Segment conectează mijlocul bazei (a doua linie de mijloc) trapezului, trece prin punctul de intersecție al diagonalelor și extinderea acesteia - intersecția prelungirile laturilor:
Segment unește punctele de centru ale diagonalelor (a treia linie centru) a trapezului, și este paralelă cu bazele lor pe jumătate:
RS = ½ (AD-BC).
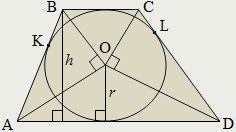
Cercul trapez poate fi înscris, în cazul în care suma ei de bază este suma laturilor:
Centrul cercului înscris în trapezul este punctul de intersecție al Bisectoarele unghiurilor interioare ale unui trapez.
Într-un ABCD trapez cu bazele AD și BC pot înscrie într-un cerc, dacă și numai dacă îndeplinește cel puțin una din ecuațiile:
Părțile laterale ale trapezului văzute din centrul cercului înscris într-un trapez, un unghi drept,
∠ = ∠ COD Chestiuni diverse = 90 °.
Raza cercului înscris în trapezului poate fi determinată:
- prin segmentele pentru a diviza partea laterală a punctului de contact:
A numit un trapez echilateral, ale cărui laturi sunt egale:
Într-un trapez echilateral:
- Unghiurile de la baza sunt:
∠ A = ∠ D. ∠ B = ∠ C;
- suma unghiurilor opuse este 180?:
∠A + ∠ C = ∠ B + ∠ D = 180 °.
Despre trapez poate fi descris ca un cerc dacă și numai dacă este isoscel.
Părțile și diagonală ale unui trapez echilateral sunt legate de:
Trapeze numit dreptunghiular, dacă una din laturile sale perpendiculare pe baza.
Zona de trapez poate fi determinată:
- prin jumătate din totalul bazelor (o primă linie de mijloc) și a altitudinii:
- prin diagonală și unghiul dintre ele:
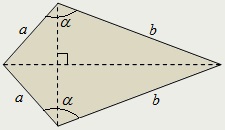
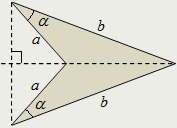
Deltoid numit un patrulater având două perechi adiacente de părți egale.
Deltoid poate fi convexă sau non-convexe.
Direct conținând orice deltoid diagonală se intersectează în unghiuri drepte.
In orice unghiuri deltoid între laturile adiacente sunt inegale.
Zona oricărui deltoidiană poate fi determinată:
- două laturi adiacente inegale și un unghi: între ele
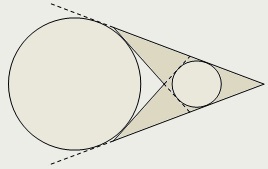
În orice deltoid convexe poate înscrie într-un cerc.
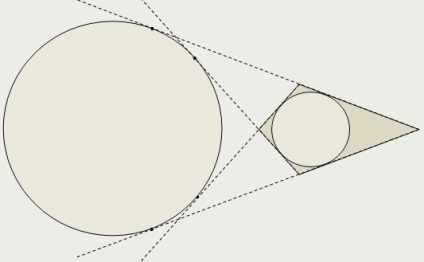
În cazul în care nu este bombat deltoid un diamant, există un cerc tangentă la extensiile de toate cele patru laturi ale deltoid.
Pentru deltoid non-convex poate construi o tangentă cerc la două laturi lungime mai mare și prelungirile două partide mai mici, precum tangenta cercul celor două părți mai mici, iar prelungirile două laturi mai mare lungime.
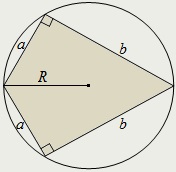
In jurul deltoid poate descrie un cerc, dacă și numai dacă inegale părți formează unghiuri de 90 °.
Raza cercului circumscris despre deltoidul poate fi definit prin cele două părți inegale:
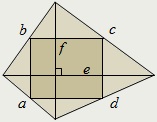
Patrulater numit ortodiagonalnym daca diagonalele sale se intersectează în unghiuri drepte.
De patrulater este ortodiagonalnym dacă și numai dacă îndeplinește una dintre condițiile:
- pentru laturile patrulaterului este adevărată: a² + c² = b² + d ²;
- pentru zona patrulaterului adevărate: S = ½ef;
- Pierre Varignon paralelogram cu vârfuri la punctele de centru ale părților laterale ale patrulaterului este un dreptunghi.
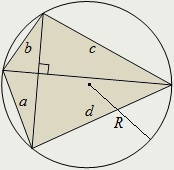
Suma pătratelor laturile opuse ale cercului înscris în patrulaterul ortodiagonalnogo egal cu diametrul pătrat al cercului circumscris:
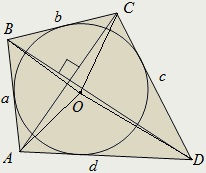
patrulater Ortodiagonalny este descrisă în jurul circumferinței dacă și numai dacă produsul dintre laturile sale opuse egal cu:
Dacă ABCD - patrulaterul ortodiagonalny circumscris un cerc centrat la punctul O. Raportul dintre adevărate:
Mult timp am planificat și în cele din urmă! Ceva de genul acesta este povestea grupului nostru VKontakte. Îndoieli cu privire la necesitatea existenței sale aruncate, iar prima comunitate materială a expus.
Se extinde funcționalitatea meniului principal.