

Pas cu pas algoritm pentru rezolvarea problemei №8 - construcția liniei de intersecție a conului și suprafețele cilindrilor
Este necesar să se construiască o linie de intersecție a suprafețelor de revoluție - un con cu un cilindru de revoluție. Axele de rotație ale acestor suprafețe sunt aranjate reciproc perpendiculare și, respectiv, sunt proiectate pe planul de proiecție.
Pentru a rezolva o astfel de problemă de geometrie descriptivă necesar să se cunoască:
- construcția suprafețelor de rotație pe o figură complexă
având în vedere coordonatele punctelor;
- cazuri speciale ale conului și intersecțiile de rotație cilindrului a planului de proiectare;
- metoda de tăiere plan pentru construcția liniei de intersecție
suprafețe.
Procedura de rezolvare a problemelor
1. Partea dreaptă a lucrării de mărime foaie de hârtie A3 conform exemplului de realizare construit eseurilor conic suprafețe și rotirea cilindrului în proiecțiile orizontale și frontale.
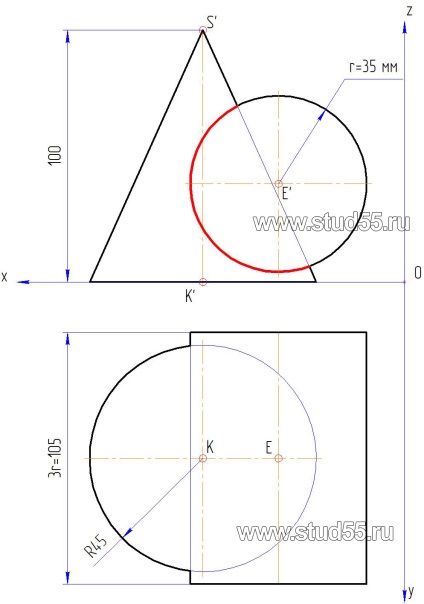
Având în vedere obținut desen ușor de văzut că aceste suprafețe de linia de intersecție este deja disponibilă în plan frontal de proiecție, adică este dat desenul sursă, selectați-l în roșu (linia dorită). Astfel, pentru a rezolva problema este de a proiecta (muta) l în plan orizontal.
2. Construcția de intersecție cu punctele de referință marca linia de start. Acesta este punctul de mai sus (mai jos) că dreapta (stânga) nu traversează linia, observăm în treacăt că linia de intersecție pot fi amplasate numai în locuri, aparținând simultan ambele suprafețe.
puncte de referință pe proiecția frontală va 1'i 6“. Găsirea proiecția lor pe orizontală prezintă nici o dificultate. Acestea vor fi pe generatoarele de capăt ale conului, care este proiectat pe acest plan o linie dreaptă Sb. Deplasându-le peste liniile de comunicare, obținem 1 U5 (ris.8.2.a).
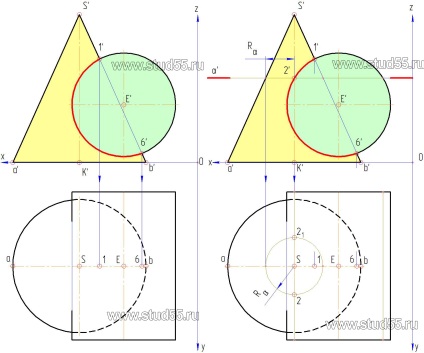
3. Apoi, aplicăm metoda planului de tăiere, care pot fi efectuate la anumite intervale de timp sau prin puncte caracteristice de intersecție a liniei care deține primul plan de tăiere „prin punctul 2“. Cazuri speciale este cunoscut faptul că în cazul în care planul de tăiere în proiecția frontală intersectează conul perpendicular pe axa de rotație, secțiunea transversală orizontală este un cerc cu raza luată de axa de rotație a suprafeței de schiță (extremă dreapta sau stânga generatoarelor). Desenați un cerc de rază Ra specificat într-un plan orizontal, plasând busola în centrul suprafeței conice. Deoarece punct2 aparține simultan conic și suprafața cilindrică este în planul intersectându, proiecție orizontală trebuie să fie amplasat în intersecția proiecțiilor orizontale ale planului de tăiere a conului și cilindru.
Am observat deja că proiecția orizontală a planului de tăiere, con - cerc; și cilindrul - o linie dreaptă. deoarece tăiere plan se extinde paralel cu axa cilindrului de rotație.
Apoi, din proiecția 2 „linia de conduită de comunicare punct (o linie de secțiune dreaptă a cilindrului), intersecția cu cercul și a obține proiecția orizontală a punctului 2. Este evident că proiecțiile punctelor vor fi două: una - pe partea din față a conului 2 (cel mai jos punct în planul orizontal de proiecție) al doilea - pe suprafața laterală din spate a conului 21 (punctul superior în planul de proiecție orizontală) (ris.8.2.b).
4. T intern în același mod găsi alte puncte ale proiecțiilor orizontale 4 și 5. adică prin frontal lor de proiecție care deține planuri de secțiune, într-un plan orizontal de proiecție - cercul respectiv pe care respectivul punct de proiecție (ris.8.3 - b).
5. Punctele de proiecție orizontale obținute sunt conectate în serie cu linia netedă a vederii, care este determinată în raport cu ambele suprafețe. Vizibilitatea este un con plin din cauza proiecției orizontale, orice punct care se află pe suprafața sa va fi vizibilă. Vizibilitatea este determinată de cilindru, astfel încât toate punctele care sunt deasupra proeminenței cilindrului alezaj frontal, vor fi vizibile pe proiecția orizontală și toate punctele situate sub diametrul cilindrului, la partea din față a proiecției - sunt invizibile cu orizontala (ris.8.3 -b).
Astfel, în planul orizontal al punctului 1, 2.3 sunt vizibile, iar punctele sunt 4,5,6 invizibile, 3 la punctul (3; 31) este o schimbare de vizibilitate. Conectarea punctului liniei de contur vizibil și punctată invizibile obține linia dorită a suprafețelor de intersecție definite.
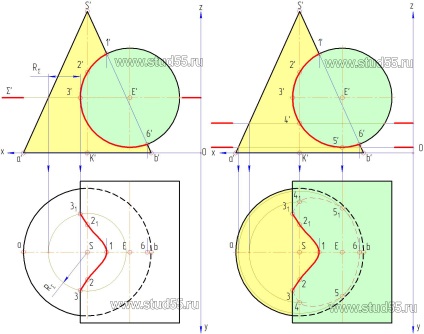
În concluzie, observăm două puncte:
1. În practică și în opțiunile de locuri de muncă se găsesc așa-numitele suprafețe complete și incomplete intersecție. Cu o intersecție parțială, în cazul în care o suprafață nu traversează complet celălalt (în acest caz), linia de intersecție există o buclă închisă; la intersecția completă atunci când o suprafață este traversează complet cealaltă, trecând linia se împarte în mai multe ramuri închise și nu vor fi la fel de mult ca zone complet intersecții suprafețe definite. Sarcinile opțiunilor propuse considerăm probleme cu intersecții de linie 2-3 buclă. Construirea de ele este la fel ca și construcție luate în considerare (ris.8.4)
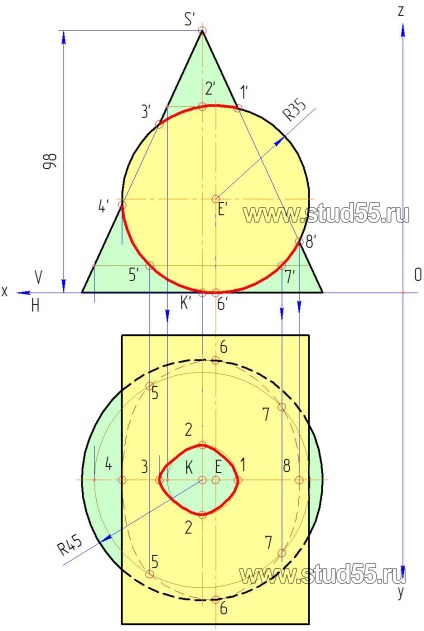
2. problema propusă la intersecția suprafețelor poate fi rezolvată prin formarea, atunci când într-o linie predeterminată de intersecție a suprafețelor se realizează un număr de generatoare, aceste puncte de intersecție sunt marcate la o linie de intersecție predeterminată, atunci aceste puncte formează împreună cu ele proiectate pe planul conjugat al proiecției.
Titlu: Geometrie descriptivă /