Cele două suprafețe care au o axă comună, numită coaxial. Suprafața Coaxial de rotație se intersectează paralele (cercuri), perpendicular pe axa de rotație. Fig. 44 sunt suprafețe coaxiale ale unui con și un cilindru. Ele se intersectează în paralel comună, care este exprimată pe planul frontal al proiecției liniei drepte perpendiculare pe axa de rotație, și orizontală - sub forma unui cerc egal cu diametrul cilindrului.
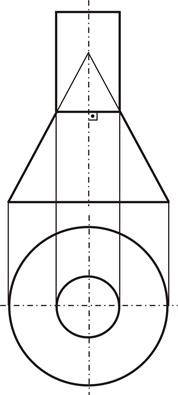
Fig. suprafață 44. Coaxial
Domeniu de aplicare - o suprafață formată prin rotirea unui cerc cu diametrul în jurul axei sale, prin aceasta poate avea este selectată o multitudine de axe de rotație. Axa de rotație a cilindrului și sferă pot fi combinate (a se vedea figura 45.) În acest caz, vom obține linia de intersecție a acestor suprafețe. - cercul perpendicular pe axa de rotație și egală cu diametrul cilindrului. Pe planul orizontal de proiecție, aceasta este reprezentată printr-un cerc ca o curbă plană închisă situată pe suprafață. Acesta va arata, de asemenea, și domeniul de aplicare al liniei de intersecție cu con. Aceste sfere de proprietate utilizate în rezolvarea o serie de probleme, în cazul în care sunt îndeplinite următoarele condiții:
1. Suprafețele Intersectarea trebuie să fie suprafețe de revoluție.
2. Axele de rotație se intersectează suprafețele trebuie să fi trecut prin punctul de intersecție al axelor poate fi realizată cu ambele sfere concentrice aceste suprafețe.
3. Axele suprafețelor trebuie să fie paralelă cu planul de proiecție, deoarece numai în acest caz paralelă intersecție secant auxiliară sferei cu suprafețe de date revoluție va fi proiectată pe planul de proiecție în formă de segmente (diametrelor cercurilor). Punctele comune acestor suprafețe, se obțin ca un punct de intersecție al paralele.
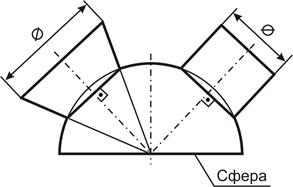
Fig. 45. Metoda de Monge
Având în vedere două suprafețe care se intersectează de revoluție. intersectându-Way sfere concentrice pentru a construi o linie de intersecție și determină vizibilitatea.
Direcții la sarcina 7
Conform Tabelului. 6, conform este selectat întruchiparea numărului figura (a se vedea paragraful. Anexa la tabelul. 6) și două proeminențe sunt construite din intersectând suprafețe.
Unghiul este dat în grade. În cazul în care nu se indică lungimea uneia dintre suprafețele, studentul își alege propriul său.
La construirea bazei cilindrului sau a conului, care este situat la un unghi față de planul de proiecție, elipsa este desenată pe două axe (vezi. Fig. 46). semiaxa mare a elipsei este egal cu diametrul bazei AB, CD - proiecția diametrului pe un plan orizontal de proiecție. Se împarte circumferința în 4 porții suplimentare. Din punctele de intersecție obținute prin diagonalele perpendiculare paralele cu axa elipsei. La intersecția acestor perpendicularele obține puncte intermediare aparținând unei elipse.
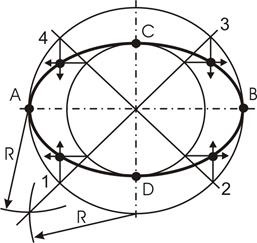
Fig. 46. Bazându-se pe două axe ale elipsei
Centrul de sfere concentrice găsi punctul de intersecție al axelor de rotație a suprafețelor și a efectuat o serie de cercuri concentrice - sfere de raze diferite.
Luați în considerare punctul de construcție 2 (vezi. Fig. 47). Din punctul de a conduce sfere cu rază arbitrară care se intersectează conul circumferențial perpendicular pe axa de rotație a conului. Traversează asemenea cilindru circumferențial perpendicular pe axa cilindrului de rotație. Intersecția acestor două cercuri este de două puncte.
Gama de raze sferelor definite de razele minime și maxime.
Raza minimă a sferei intersectând se determină din condiția sferelor de tangență care traversează una de alta și suprafețele care se intersectează.
în Rmin la cele două puncte de pe suprafața conică C2D2 circumferința. intersectează suprafața cilindrică a E2F2 circumferință. Două puncte și intersecția acestor cercuri sunt puncte de intersecție a liniei dorite.
Raza maximă este un segment de linie din centrul sferei la punctul cel mai îndepărtat de intersecție a suprafețelor intersectate de eseuri.
În acest exemplu, Rmax este egală cu distanța de la centrul de O2 al sferei de proiecție până la punctul cel mai exterior 12.
Pentru a construi celelalte puncte de intersecție ale liniei petrec mai multe sfere concentrice centrate în punctul O2. în care raza R a sferelor ar trebui să varieze
Construcția liniei de intersecție a proiecției orizontale construite pe una dintre suprafețele. În acest exemplu, este mai convenabil să se utilizeze o suprafață circumferențială conică, ca ele nu sunt distorsionate pe planul punctului de proiecție B2 aparține generatoarea schiță a cilindrului. Prin urmare, proiecția orizontală a punctului B2 se va separa o parte vizibilă și invizibilă a liniei de intersecție.
Problema este rezolvată în două proiecții.
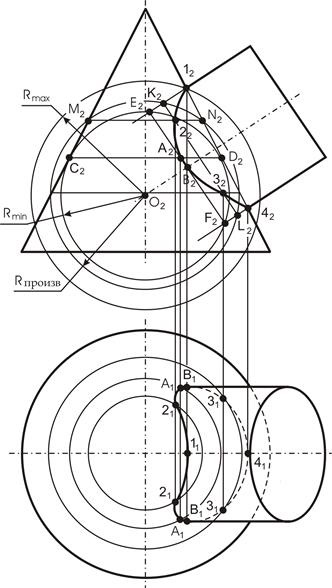
Fig. 47. Metoda sferelor