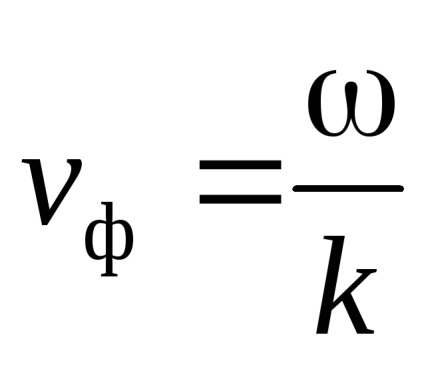

Non-dispersive mediului
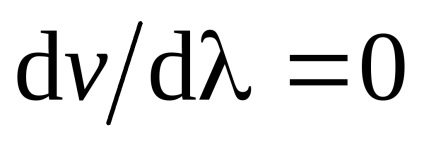
Conceptul de viteza de grup este foarte important, deoarece apare exact atunci când este măsurată în gama de radar în spațiu obiecte sisteme de management, etc. Teoria relativității se dovedește că skorostu grup
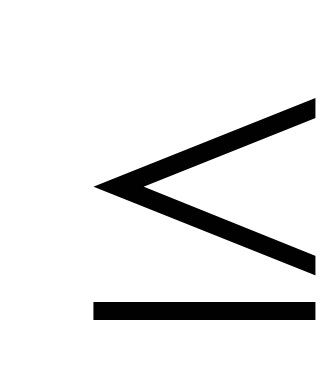
5. Interferența undelor
Se numește interferență coerentă în timp și spațiu să curgă mai multe procese de undă, care se obține prin adăugarea câștigului sau atenuarea undei rezultante.
Interferența asociată cu conceptul de coerență. Valurile numit coerent atunci când diferența de fază la fiecare punct în spațiu este menținută constantă în timp.
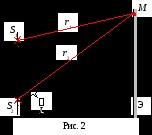
Fie ecuația două valuri sferice coerente sunt suprapuse unul pe celălalt, sunt date sub forma
S1 =
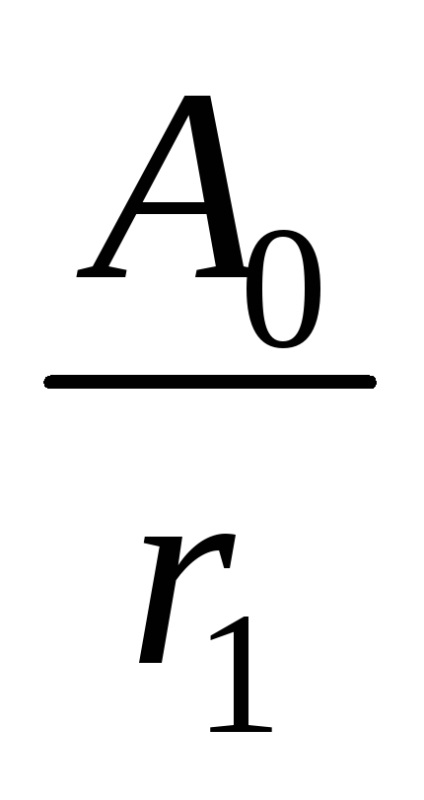
S2 =
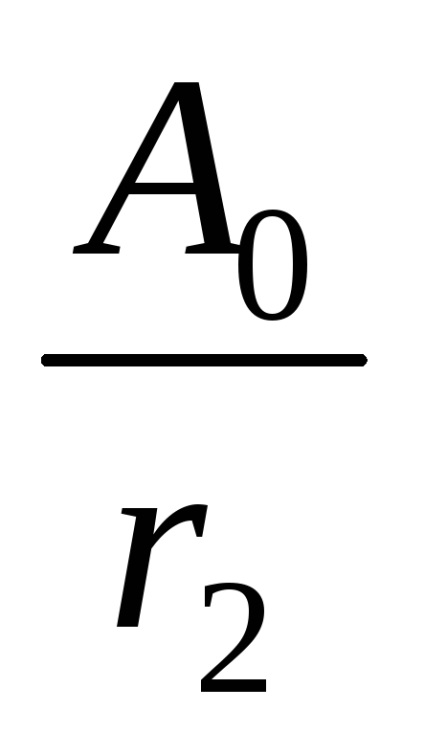
Amplitudinea undei rezultat
Deoarece pentru surse coerente diferență dintre fazele inițiale (1 2) = const, rezultatul adăugării de oscilație depinde de accident vascular cerebral val diferență
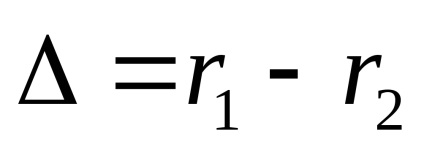
Stare maximă Interferența
amplitudinea-re Dhul fluctuațiile tiruyuschego
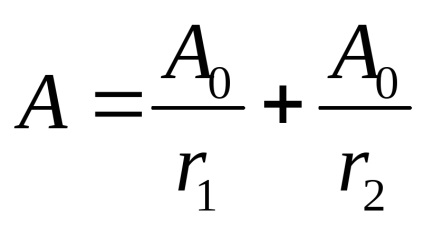
minimă interferență Stare
amplitudinea oscilației rezultată
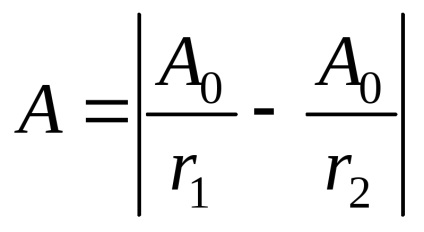
mporyadok interferență maximă sau minimă.
undele stationare
Undele permanent sunt un caz particular de interferență și sunt formate prin suprapunerea două valuri care călătoresc se propagă în direcții opuse cu frecvențe și amplitudini identice.
Adăugarea acestor ecuații și ținând cont de faptul că k = 2 / , obținem



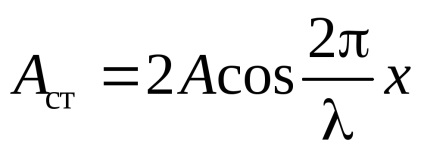
Punctele la care amplitudinea de oscilație este maximă (Ast = 2A) nazyvayutsyapuchnostyami undă staționară, iar punctul în care amplitudinea de oscilație este zero (Ast = 0) uzlami undă staționară.
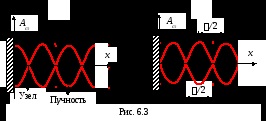
coordonate ventrele
Coordonatele nodurilor
Formarea undelor staționare observate la interferența de călătorie și reflectate valuri. Ce se întâmplă pe reflectare a frontierei sau ventru uzel depinde de raportul de densitate medie. În cazul în care mediul din care se produce mai puțin densă în locul reflexiei reflexiei se obține ventru dacă mai densă - nod. În cazul în care energia nu este transferată la valul în picioare.
Propagarea unui impuls val longitudinal pe tija elastică.
O trăsătură caracteristică a undelor mecanice este că acestea sunt distribuite într-un mediu tangibil (solid, lichid sau gazos). Există valuri care se pot propaga în vid (de exemplu, undele de lumină). Pentru unde mecanice neapărat nevoie de un mediu, având capacitatea de a stoca energia cinetică și potențială. Prin urmare, mediul trebuie să fie inert și posedă proprietăți elastice. In mediile reale, aceste proprietăți sunt distribuite în întregul volum. De exemplu, orice mic element de corp rigid are o masă și elasticitate. Cel mai simplu model unidimensională a unui corp rigid poate fi reprezentat ca un set de bile și arcuri (Fig. 2.6.3).
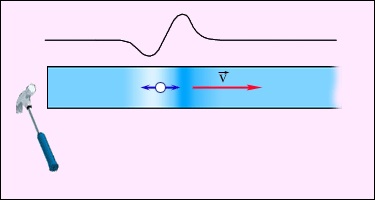
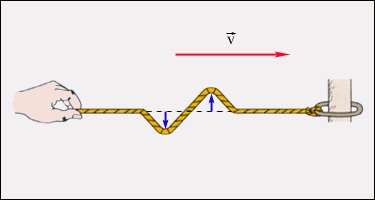
Un model simplu unidimensională a unui corp rigid.
In acest model, proprietăți inerte și elastice sunt împărțite. Granulele au o masă m. si arcuri - k rigiditate. Cu un astfel de model simplu pentru a descrie propagarea undelor longitudinale și transversale în solide. În valuri longitudinale bile se confruntă cu deplasarea de-a lungul lanțului, iar arcurile sunt întinse sau comprimate. Această deformare se numește o deformare de compresiune sau întindere (vezi. §1.12). Lichide sau gaze de acest tip este însoțită de o deformare a sigiliului sau a vidului.
unde mecanice longitudinale se pot propaga in orice mediu - solide, lichide și gazoase.
Dacă deplasarea în direcție perpendiculară pe lanț, există o deformare de forfecare în modelul unidimensional unui solid, una sau mai multe bile. Deformează în timpul acestei deplasări a arcului va tinde să se întoarcă în poziția deplasată a particulelor de echilibru. În acest caz, următoarele particule imparțiale vor acționa forțe elastice care doresc să-i abată de la pozițiile lor de echilibru. Ca rezultat, lanțul rula de-a lungul undei transversale.
Lichidele și gazele de forfecare elastic deformare nu se produce. Dacă un strat dintr-un fluid pentru a deplasa o distanță oarecare în raport cu un strat adiacent, nu există forțe tangențiale la interfața dintre straturi nu apare. Forțele care acționează asupra interfeței dintre un lichid și un solid, iar forțele între straturile adiacente de fluid sunt întotdeauna direcționate de-a lungul normala la limita - această forță de presiune. Același lucru este valabil și pentru mediul gazos. În consecință, undele transversale nu pot exista în medii lichide sau gazoase.
un interes considerabil în practică sunt valuri armonice sau sinusoidale simple. Ele sunt caracterizate prin oscilații particule amplitudoyA chastotoyf și lungimea de undă valoarea:. unde sinusoidale se propagă în mediu omogen, cu o viteză constantă υ.
Deplasarea y (x. T) a particulelor medii din poziția de echilibru într-o undă sinusoidală depinde de coordonate x pe axa OX. a lungul căreia unda se propagă și timpul t conform legii:
în cazul în care - după cum nazyvaemoevolnovoe număr. ω = 2πf - frecvența circulară.
Fig. 2.6.4 emisiuni „instantanee“ ale undei transversale la două momente de timp: t și t + At. In timpul val mutat de-a lungul At axa OX de o υΔt distanță. Valuri, toate punctele de care se deplasează cu aceeași viteză, de obicei, numit de funcționare (spre deosebire de picioare valuri cm. De mai jos).
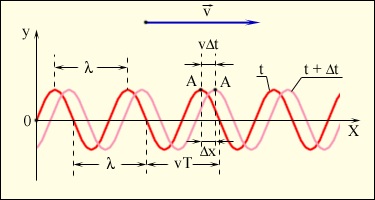
„Instantaneu“ al o undă sinusoidală de călătorie la momentul t și t + At.
Wavelength λ se numește distanța dintre două puncte adiacente de pe axa OX. oscilant în aceleași faze. O distanță egală cu lungime de undă X, unda variază în timpul perioadei T, prin urmare, λ = υT. unde υ - viteza de propagare a undei.
Pentru orice punct selectat pe graficul procesului de undă (de exemplu, la punctul A din figura 2.6.4.) La ωt expresie - kx nu se schimbă în dimensiune. Cu trecerea timpului t și modificări x punctului de coordonate. După un interval de timp punctul A se deplasează AT pe axa OX la o oarecare distanță = υΔt Ax. Prin urmare:
Modelul. unde longitudinale și transversale.
În cazul în care unda mecanică propagă în mediu, se întâlnește în calea sa un obstacol, se poate schimba drastic natura comportamentului. De exemplu, unda se reflectă parțial la interfața dintre două medii cu proprietăți mecanice diferite, și pătrunde parțial în al doilea mediu. Wave călătorind de-a lungul unui șir de bandă sau de cauciuc reflectată de la capătul montat fix; astfel, există un val care călătoresc în direcția opusă. Șirul este fixat la ambele capete, există oscilații complexe care pot fi considerate ca o superpoziție (superpoziție) din cele două valuri care călătoresc în direcții opuse și sunt supuse reflecții și reflecții multiple la capete. Vibrațiile unui șir de caractere fixat la ambele capete, creând sunetele tuturor instrumentelor de coarde. Un fenomen similar se produce atunci când sunetul instrumentelor de suflat, inclusiv conductele de organe.
Dacă undele călătoresc de-a lungul șirului în direcții opuse, au o formă sinusoidală, ele pot forma un val în picioare în anumite condiții.
Lăsați șirul de lungime l este fixat astfel încât unul din capetele sale este situat la x = 0, iar celălalt - (. Figura 2.6.5) la x = l. Tensiunea șir creată T.
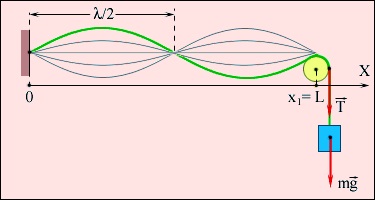
Formarea unui val în picioare într-un șir de caractere fixat la ambele capete.
Șirul aplică simultan două valuri în direcții opuse la aceeași frecvență:
La punctul x = 0 (unul dintre capetele fixe ale șirului) al y1 undei incidente de unda de reflexie genereaza y2. La reflecție de la capătul montat fix al undei reflectate este defazat cu incidentul. Conform principiului superpoziției
Acesta este un val în picioare. Într-un val în picioare, există puncte fixe numite noduri. La jumătatea distanței dintre nodurile sunt puncte care variază cu amplitudinea maximă. Aceste puncte sunt numite ventrele.
Două capete fixe ale șirului trebuie să fie noduri. Cele de mai sus Formula satisface această condiție la capătul stâng (x = 0). Pentru a îndeplini această condiție și la capătul din dreapta (x = l), este necesar ca kl = n π, unde n - orice număr întreg. Aceasta înseamnă că unda de picioare are loc în șirul nu este întotdeauna, dar numai în cazul în care lungimea I a șirului este egal cu un număr întreg de jumătăți de valuri:
Un set de valori ce corespund setului de lungimi de undă λn de frecvențe posibile fn:
în cazul în care - viteza de propagare a undelor transversale pe coardă. Fiecare dintre frecvențele de vibrație de tip string nazyvaetsyanormalnoy moda asociat. Cea mai mică frecvență se numește f1 frecvență fundamentală. toate celelalte (F2. F3. ...) numite armonici. Fig. 2.6.5 ilustrează moda normal pentru n = 2.
Unda în picioare este nici un flux de energie. energia vibrațională conținută într-o secțiune a unui șir între două noduri adiacente, nu este transportat în alte părți ale șirului. Fiecare astfel de segment este periodic (de două ori pe perioada T) conversia energiei cinetice în energie potențială și invers ca în sistemul oscilatorie convențional. Dar, spre deosebire de sarcina pe arcul sau pendulul, în care există doar o singură frecvență naturală a șirului are un număr infinit de naturale chastotfn (rezonanță). Fig. 2.6.6 descrie mai multe tipuri de picioare valuri într-un șir de caractere fixat la ambele capete.
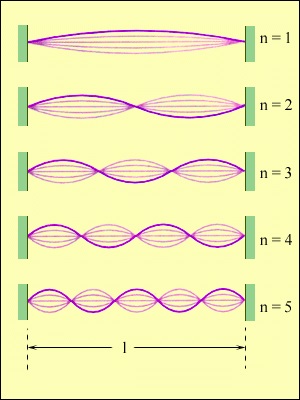
Primele cinci moduri normale de vibrații ale unui șir fix la ambele capete.
În conformitate cu principiul superpoziției undelor de diferite tipuri în picioare (adică. E. valori diferite ale lui n) pot fi prezente simultan în vibrațiile șir.