Să presupunem că un corp sub forța F, aplicată la punctul A este adus în rotație în jurul axei OO „(fig. 1.14).
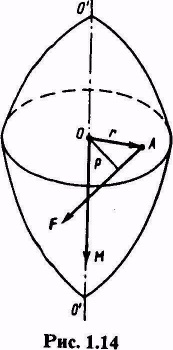
In prezent silyest vectorul definit de produsul vectorial al vectorului raza punctului de aplicare a forței și vectorul forței:
(3.1)
Unitatea de forță momentul - newton-metru (N • m).
Direcția M pot fi găsite folosind regula șurubului din dreapta.
momentul Impulsachastitsy este un produs vectorial al particulei vector raza pe elanul:
sau L = un scalar gPsin # 945;
Această mărime vector și aceeași direcție ca și vectorii # 969;.
§ 3.2 Momentul de inerție. Teorema lui Steiner
Măsura de inerție a organelor la deplasarea înainte a unei mase. corp Inerția în timpul mișcării de rotație nu depinde numai de masa, ci și pe distribuția în spațiu în raport cu axa de rotație. Măsura de inerție atunci când mișcarea de rotație este o valoare Du- numitul moment de inerție în jurul axei de rotație.
Momentul de inerție al punctului material în raport cu axa de rotație-TION este produsul masei punctelor pe pătratul distanței de la axa sa:
Momentul de inerție în raport cu axa de rotație se numește mente sumă mo de inerție ale punctelor de masă din care corpul include:
Momentul de inerție al corpului depinde de o relativă axa se rotește și este distribuit ca greutate în volum.
Cel mai simplu determinat de momentul de inerție al corpurilor, având formă geometrica regulată și distribuție uniformă a greutății în volum.
· Momentul de inerție al unei tije uniform în jurul unei axe care trece prin centrul de inerție și perpendicular pe tija
· Momentul de inerție al unui cilindru uniform în jurul unei axe perpen-dikulyarnoy bază și care trece prin centrul masei sale,
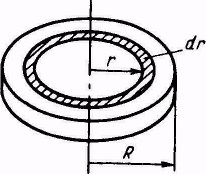
· Momentul de inerție al unui cilindru cu pereți subțiri sau înveliți în jurul unei axe perpendiculare pe planul bazei sale și care trece prin centrul său,
· Momentul de inerție diametrul mingii
sunt furnizate Formulele pentru momentele de inerție corpurilor, ca axa de rotație trece prin centrul de masă. Pentru a determina momentele de inerție față de o axă arbitrară, folosește teorema lui Steiner: momentul de inerție față de o axă arbitrară de rotație este egal cu suma momentului de inerție față de o axă paralelă cu aceasta care trece prin centrul de masă, iar greutatea produsului pe pătratul distanței dintre axe:
[M - masa corpului, d - distanța de la centrul de masă la selectat axa Vera-scheniya (distanța între axe)].
inerție unitate - kilogram-metru pătrat (kg • m 2).
Astfel, momentul de inerție al unei tije uniform în jurul unei axe care trece prin extremitatea sa pe teorema lui Steiner este
§ 3.3 Ecuația dinamicii de rotație a mișcării a corpului rigid
Luați în considerare primul punct material A m în masă, se deplasează de-a lungul circumferinței raza r (fig. 1.16). Să forța ei constantă F, direcționată de-a lungul tangenta la cercul. Conform legii a doua a lui Newton, această forță este accelerația tangențială, sau F = ma # 964; .
Folosind raportul unei # 964; = # 946; r. Obținem F = m # 946; r.
Înmulțind ambele părți ale ecuației scrise mai sus pentru r.
Fr = m # 946; r 2. (3.13)
Partea stângă a expresiei (3.13) este momentul forței M = Fr. Partea dreaptă este produsul accelerației unghiulare # 946; în momentul de inerție al materialului punctului A: J = m r 2.
Accelerația unghiulară a punctului în timpul rotației sale în jurul unei axe fixe este proporțională cu cuplul și invers proporțională cu momentul de inerție (ecuația dinamică de bază a mișcării de rotație a punctului material):
M = # 946; Sau J (3.14)
Când constantă forța de rotație a cuplului a accelerației unghiulare este o valoare constantă și poate fi exprimată în termeni de diferență între vitezele unghiulare:
Apoi, ecuația de bază a dinamicii mișcării de rotație poate fi scrisă ca
[Este momentul pulsului (sau momentul unghiular), M # 916; t - un cuplu de impulsuri (sau cuplul de impuls)].
Ecuația fundamentală a dinamicii mișcării de rotație poate fi scrisă ca
§ 3.4 Legea conservării momentului cinetic
Luați în considerare cazul frecventă a mișcării de rotație, atunci când momentul total al forțelor exterioare este zero. Când mișcarea de rotație a corpului fiecare dintre mișcările de particule cu o viteză lineară # 965; = # 969; r, [r, - raza cercului care descrie particula-masa este m, # 969; - viteza unghiulară egală pentru toate punctele din organism].
Momentul de impuls al unui corp de rotație este egală cu suma momentelor
particule individuale pulsurilor:
Schimbarea momentului cinetic este egală cu impulsul de cuplu:
În cazul în care durata totală a tuturor forțelor exterioare care acționează asupra sistemului corpului în raport cu o axă fixă arbitrară este egal cu zero, adică, M = 0, dl, iar suma vectorială a sistemului de impulsuri corpurile momente nu se schimbă cu timpul.
Valoarea momentului cinetic al tuturor organismelor sistemului izolat rămâne neschimbată (legea conservării momentului cinetic):
d (J # 969;) = 0 J # 969; = const (3,20)
Conform legii conservării momentului cinetic poate fi scris
unde J1 și # 969; 1 - momentul de inerție și viteza unghiulară la momentul inițial, și J2 și # 969; 2 - în timpul t.
Din legea conservării momentului cinetic rezultă că M = 0 în sistemul de rotație în jurul axei de orice modificare a distanței de la organele la axa de rotație ar trebui să fie însoțită de schimbări în viteza lor în jurul acestei axe. Odată cu creșterea distanței de viteza de rotație scade cu o scădere - creștere. De exemplu, o gimnastă care efectuează tumbe pentru a obține făcut în aer câteva ture în timpul balului salt de coagulare. Balerina sau patinatoare, încercuind în piruetă, se întinde brațele, dacă el vrea să încetinească rotația, și, dimpotrivă, le presează la corp, atunci când încearcă să se rotească cât mai repede posibil.
§ 3.5 Energia cinetică a unui corp rotativ
Noi definim energia cinetică a corpului solid se rotește în jurul unei axe fixe. Noi împărțim corpul la punctele de masă n. Fiecare punct se mișcă cu viteză liniară # 965; i = # 969; ri. apoi energia cinetică a unui punct
Energia cinetică totală a unui corp rigid de rotație este egală cu suma energiilor cinetice ale tuturor punctelor sale materiale:
(J - momentul de inerție în raport cu axa de rotație)
Dacă traiectoriile tuturor punctelor se află în planuri paralele (ca în cilindru, alunecarea în jos din planul înclinat, fiecare punct este mutat în figura planul său), această mișcare plană. În conformitate cu principiul mișcării planul Euler poate fi întotdeauna nenumărate moduri descompusă în mișcare de translație și de rotație. În cazul în care mingea cade sau slide-uri de-a lungul planului înclinat, se deplasează numai în mod progresiv; atunci când mingea este de rulare - și este încă de rotație.
În cazul în care organismul realizează de translație și o mișcare de rotație în același timp, energia cinetică totală este
Dintr-o comparație a energiei cinetice a formulelor pentru a doua translație și rotație mișcările se poate observa că o măsură de inerție la rotație mișcarea este Tel'nykh moment de inerție.
§ 3.6 Activitatea forțelor externe în timpul rotației unui corp rigid
Atunci când un corp rigid se rotește, energia potențială nu se schimbă, astfel încât activitatea elementară a forțelor externe este egală cu creșterea energiei cinetice a corpului:
Având în vedere că J # 946; = M, # 969; dr = d # 966;, au
# 916; A = M # 916; # 966; (3.24)
Munca forțelor externe în rotație a corpului rigid printr-un unghi finit # 966; este
Când rotația în stare solidă în jurul unei axe fixe de lucru prin acțiunea forțelor externe, momentul acestor forțe în raport cu această axă. În cazul în care cuplul în jurul axei este zero, aceste forțe nu produc lucru.