Toate Fractură reale. Sub influența forțelor aplicate, se schimbă forma sau volumul lor. Astfel de modificări sunt numite tulpini. În cazul substanțelor solide, există două cazuri de limitare: deformare elastică și deformare plastică. Chemat de deformare elastică, dispare după încetarea forțelor aplicate. deformarea plastică sau permanentă se numește tulpina astfel încât persistă în organism, cel puțin parțial, și după încetarea forțelor exterioare aplicate. Este deformarea plastică elastică sau - aceasta depinde nu numai de material corpului, dar, de asemenea, cu privire la magnitudinea forțelor aplicate. Dacă forța (mai precis, forța pe unitatea de suprafață, adică tensiune) nu depășește o valoare cunoscută numită limită elastică. atunci deformarea rezultată va fi elastic. În cazul în care depășește această limită, deformarea rezultată este din material plastic. Separarea corpurilor pe elastic și plastic într-o oarecare măsură, arbitrară. Strict vorbind, toate tulpina după încetarea forțelor externe nu este dispărea complet, așa că sunt din plastic.
Diferitele părți ale corpului deformate interacționează unul cu altul la interfețele de-a lungul care se sprijină unul pe altul. Luați în considerare un organism deformat arbitrar sau de mediu. împărțiți Mintal două părți ale sale: corpul și corpul I al II-lea. se invecineaza reciproc de-a lungul suprafeței AB (Fig. 13). pentru că Am deformat corpul, acționează asupra organismului II cu o anumită forță. În consecință corpul II acționează asupra corpului I cu aceeași, dar oppositely îndreptate forța. Cu toate acestea, pentru a determina deformarea care apar în același timp, este necesar să se cunoască modul în care aceste forțe sunt distribuite pe secțiunea transversală. Ia suprafață AB dS zona infinitezimal. Să - o forță care să fie pe acest corp platformă II acționează asupra corpului I. Forța per unitate de suprafață, de exemplu, . Se numește tensiune. acționând la un punct de pe frontiera AB. dS zona de orientare poate fi stabilită prin specificarea direcția normală la acesta. Să presupunem că normală este îndreptată către exterior din suprafața corpului la care acționează forță. Notăm vectorul unitar al unui, bine normală - tensiunea nominală. Vectorul poate fi descompus într-o componentă de-a lungul n normale și componenta situată în planul tangent la site-ul dS. Prima componentă se numește normală. iar al doilea - o subliniază tangențiale care acționează pe site-ul dS.
Ia-rod uniform și atașați la aceasta tracțiune motive sau forță de compresiune F (fig. 14, a și b). Tija va fi deformată, și anume, comprimat sau întins. Forța pe unitatea de suprafață în secțiune transversală, se numește stres. În acest caz, o tensiune perpendicular pe secțiunea transversală a tijei. În cazul în care tija se prelungește, se numește o tensiune și stres este dat de
unde S - aria secțiunii transversale a barei. Dacă tija este comprimat, presiunea și stresul se numește definit numeric prin aceeași formulă
Este ușor de observat că.
Să L0 - lungimea unstrained a tijei. După aplicarea lungimii forței F este incrementată # 916; l și devine l = l0 + # 916; l. atitudine
Se numește alungirea tijei. În cazul extinderii este pozitiv în compresie - este negativ.
Experiența arată că deformări prea mari elastice ale T tensiune (sau presiunea P) este proporțională cu alungirea relativă (relativă sau compresiune).
unde E - o constantă în funcție numai pe tija de material și starea sa fizică. Se numește modulul lui Young. Aceste formule exprimă legea lui Hooke pentru sușă sau compresie tije de tracțiune. Această lege aproximative și pentru deformări mari, nu se poate rula. Deformarea, pentru care Legea lui Hooke deține aproximativ, numit deformări mici. Mai general, decât legea lui Hooke, care este afirmația că, în cazul unor deformații elastice ale T tensiune este o funcție lipsită de ambiguitate de alungire # 949; .
Se pare că, în cazul în care deformarea este mic, constantele elastice ale organelor nu se modifică în deformări. Astfel, în cazul în care organismul are mai multe forțe, pentru a calcula deformarea rezultată poate fi calculată mai întâi tulpina cauzată de forță în fiecare individual (ca și în cazul în care alte forțe nu au fost deloc), iar apoi deformarea rezultată pliat. Această poziție se numește principiul superpoziției deformațiilor mici.
Energia elastică este întinsă bar
Densitatea în vrac a energiei elastice; u energie elastică. per unitate de volum al Lungită (sau comprimat) al tijei, este egală cu
Dacă vom folosi legea lui Hooke, această expresie poate fi redus la forma
Experiența arată că, în conformitate cu o întindere sau compresiune schimbare forță F nu numai longitudinal, ci și dimensiunile transversale ale tijei. Dacă forța F - întindere, dimensiunile transversale ale barei sunt reduse. Dacă se micșorează, acestea sunt în creștere.
Să a0 - grosimea tijei de zis deformarea, și - după deformare. Pentru grosimi pot fi luate pentru diametrul bare rotunde, o formă dreptunghiulară - una dintre laturile bazei sale, etc. Dacă forța de tracțiune F, valoarea se numește tija relativă compresiune transversală (# 916; a = a - a0). Relația în raport cu contracție transversală alungirea longitudinală relativă corespunzătoare numit raportul Poisson
Raportul Poisson depinde numai de materialul corpului și este una dintre cele mai importante constante care caracterizează proprietățile sale elastice.
Modulul lui Young E și raportul Poisson # 956; caracteriza pe deplin proprietățile elastice ale unui material izotrop. Toate celelalte constante elastice pot fi exprimate în termeni de E și # 956; .
Astfel, deformarea elastică a solidelor este descrisă de Hooke
unde s = F / S - efort normal (raportul dintre forța F. prilozhennoyperpendikulyarno secțiune transversală a eșantionului aria S a secțiunii transversale); - deformarea relativă (raportul de alungire a Soacra cu originalul l0 lungimea probei), E - modulul de elasticitate (modulul lui Young) .Zametim că s este numeric egală cu energia per 1 m 3 dintr-un material deformabil.
modulul lui Young caracterizează proprietățile elastice ale solidelor sub presiune la tracțiune - compresiune. Este numeric egală cu valoarea tensiunii care determină o schimbare în lungime de probă de două ori, în cazul în care deformarea în acest caz este elastică. Pe de altă parte, modulul Young poate fi înțeleasă ca o valoare care este numeric egală cu energia de deformare volumetrica prin dublarea dimensiunii eșantionului.
legea lui Hooke este valabilă numai pentru corpurile perfect elastice. există diverse abateri de la această lege pentru aceleași organisme reale. Fig. 15 este o diagramă caracteristică a unui corp solid de întindere. proporționalitate strictă între alungire și tensiune observate numai la sarcini relativ mici pe zona 0A.
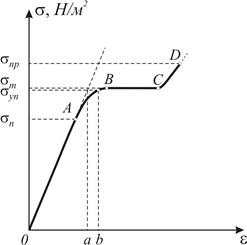
Fig. Figura 15. tulpina solidă
voltaj # 963; n. în care legea lui Hooke, numită limita de proporționalitate.
sup maximă tensiune. în care nu apar încă o deformare reziduală (reziduală relativ deformatsiyane prevyshaet0,1%) se numește limita de elasticitate. Acesta corespunde punctului B din deformarea diagrama.
Randament - o tensiune care caracterizează o stare a corpului deformabil, după care alungire este crescută, fără a crește forța de operare (segment orizontal BC).
spr Rezistența la tracțiune (punctul D), se numește o tensiune corespunzătoare celei mai înalte sarcină a rezistat de organism înainte de spargere.
Abaterile de la legea lui Hooke în tensiune care nu depășește limita elastică, este lipsa de elasticitate generală noțiune. Manifestare inelasticitatea sunt, de exemplu, aftereffect elastic și histerezisului elastic. sub rezerva observațiilor experimentale în acest studiu.
Fenomenul de primăvară din spate este de a schimba starea de deformare în timp, la o valoare constantă de tensiune. În acest caz, după aplicarea sarcinii la deformarea probei nu se produce instantaneu, dar continuă să crească cu timpul (încovoierii directe); De asemenea, după îndepărtarea sarcinii: deformarea modelului nu dispare imediat, și a continuat să scadă în timp (încovoierii inversă).
Zona delimitată de curba de sarcină și două abscise corespunzând la două valori ale tulpinii este proporțională cu A sau forțele externe, care, de asemenea, potențialul energetic E în deformarea elastică a eșantionului. Acest lucru rezultă din zona DQ calcul sub elementul curbă
în cazul în care un - coeficient de proporționalitate, DW1 - densitatea volumetrică a energiei de deformare a probei. Coeficientul de proporționalitate este egal cu densitatea volumetrică susa de energie pe unitatea de suprafață delimitată de graficul și are dimensiunea J / celulă.
Aria de sub curba corespunzătoare întregului volum de încărcare W1 densitatea de energie. și aria de sub curbă întreaga descărcare - W2 densitatea de energie de volum.
Dacă proba aplicat pentru prima tensiune în creștere și apoi descărca, apoi graficul s = f (e) curba de încărcare nu va coincide cu ramura de descărcare. La ciclu de încărcare completă - formulare Graficul de descărcare o figură numită o buclă de histerezis. buclă proporțională pătrat pentru densitatea aparentă a energiei elastice DW absorbită. a trecut în căldură.
Fenomenele conversia ireversibilă a energiei mecanice în căldură (în caz contrar, disiparea energiei) în procesele de deformare a solidelor din cauza așa-numita frecarea internă.
Pentru a cuantifica frecarea internă a materialelor folosite adesea valoare relativă - coeficient de absorbție
în cazul în care W1 - energie elastică în timpul încărcării probei.
Fenomenul inelasticitatea inerent tuturor solidelor reale cu greutate moleculară joasă și polimer, inclusiv metale.
Fenomene metale inelasticitatea și alte materiale cristaline asociate cu defecte zăbrele: diferite defecte punctiforme, dislocările și neregularități cauzate de structura lor și, în consecință, prezența microstrain mecanice interne în solide. material polimeric Unelasticity datorită modificărilor structurilor macromoleculare sub stres mecanic.
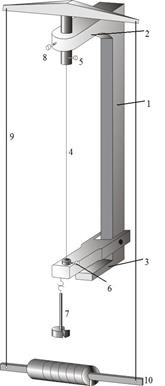
Fig. 16. Configurația experimentală
Instalație pentru sușa monitorizare la întindere este prezentată în Fig. 16. Se compune dintr-o bază masivă 1 2 cu superioare și inferioare consolele 3. probă de testare - fir 4 este fixat cu ajutorul șurubului de cleme 5 și 6. inferioară Clema platformă fixă 7, pe care sunt aplicate sarcinile pentru a construi sarcina. Pentru comoditatea de fixare a firului pendular superior deplasabil și poate fi fixat cu ajutorul șurubului 8. Pentru partea superioară a brațului în timpul măsurării a fost sub sarcină constantă și a avut un cot permanent, să-l pe tijele 9 suspendate de o curea orizontală 10. La aceasta, înainte de măsurători sunt montate toate sarcinile care sunt apoi transmise la platforma. Set dispozitiv (de obicei fixat pe perete), în poziție verticală.
Pentru măsurarea precisă a cantității tulpinii aplicată la cathetometer.
Cathetometer este utilizat pentru măsurarea segmentelor verticale dispuse la distanțe
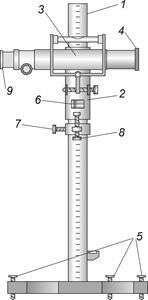
Fig. 17. cathetometer dispozitiv schematică.
câteva zeci de centimetri de la telescopul cathetometer obiectiv.
Cathetometer (Fig. 17) constă dintr-o coloană verticală cu trepied trepied 1, căruciorul de măsurare 2, telescopul 3 și 4. Indicatorul de măsurare microscop de ridicare a rotorului 5 coloană trepied poate fi montat pe plan circular vertical. C poate fi rotit în jurul unei axe verticale prin intermediul coloanei 6 stilouri. Căruciorul de măsurare 2 transportă telescopul 3 și 4 cu un microscop de citire este deplasată de-a lungul coloanei pe role. mișcarea verticală grosieră a transportului este purtat de mâini când unfastening șurubul 7, curent - printr-un șurub micrometric 8 atunci când șurubul 7 fix.
Telescopul 3 este fixat la căruciorul. Concentrându tuburi la punctul obiect selectat se realizează prin rotirea laterală a volantului 9. Tubul are un nivel cilindric, a cărui axă este paralelă cu axa de vizare a tubului. Acesta poate fi setat într-o poziție orizontală de imaginile micrometru cu șurub care combină toate veziculei vizualizate prin ocular telescop. La combinarea jumatati axa telescop cu bule de vizare ia poziție strict orizontală.
Cathetometer sistem de măsurare constă dintr-un indicator telescop și microscop de măsurare cu un sistem de iluminare. În planul focal al ocularului microscopului este setat măsurarea grilă indicator scală (fig. 18), pe care un dispozitiv optic special proiectat scala milimetrica. Măsurarea distanțelor între două puncte se realizează prin indicatorul telescop și microscop măsurarea prin compararea lungimii măsurate cu scala milimetrică.
Fig. 18. O grilă cathetometer scară
Fig. 19. bisector
Deplasarea căruciorului cu telescopul, și un microscop pentru coloana de referință de-a lungul scalei milimetrice și rotirea coloanei în jurul axei verticale a țevii setat la punctul obiectului selectat; probele sunt îndepărtate prin ocular indicatorului de măsurare microscop pe scară și grila scară. Lungimile segmente verticale se determină ca diferența dintre probele respective pe o scală.
Cathetometer este prevăzut cu un transformator pentru încorporarea într-o parte de iluminare de măsurare rețea microscop indicator.