principal nbsp> nbsp Wiki-Tutorial nbsp> nbsp matematică nbsp> clasa nbsp10 nbsp> nbspReshenie inegalități trigonometrice simple: Exemple și algoritmi
Inegalitatile care implică funcții trigonometrice, în abordarea inegalităților sunt reduse la cele mai simple cos tip (t)> o, sint (t) = a și altele asemenea. Și chiar mai simplu de inegalitate sunt rezolvate. Luați în considerare diferite exemple de cele mai simple moduri de a rezolva inegalitățile trigonometrice.
Exemplul 1 Pentru a rezolva păcatul inegalitatea (t)> = -1/2.
Desenați un cerc unitate. Deoarece sin (t) prin definiție - o coordonată y, notați punctul de pe axa y y = -1 / 2. Atragem prin ea o linie paralelă cu axa x. Intersecția liniei drepte cu programul de cercul unitate marchează punctul PT1 și Pt2. Am conecta cele două segmente de origine la punctul PT1 și Pt2.
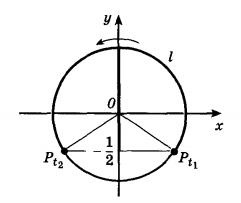
Soluția acestei inegalități va avea toate punctele unității dispuse deasupra punctelor de date cerc. Cu alte cuvinte, decizia va fi arc l. Acum, trebuie să specificați condițiile în care un punct arbitrar va aparține unui arc de cerc l.
PT1 este in semicercul dreapta, ordonata sa egala cu 1/2, apoi t1 = arcsin (-1/2) = - pi / 6. putem scrie următoarea formulă pentru a descrie punctul PT1:
t2 = pi - arcsin (-1/2) = 7 * pi / 6. Ca rezultat, obținem pentru T următoarea inegalitate:
Ne rezervăm semnele de inegalitate. Și astfel ca o funcție a funcției sinus este periodică, atunci decizia va fi repetată la fiecare 2 * pi. Această condiție se adaugă la inegalitatea rezultată pentru T și scrie răspunsul.
Răspuns: pi / 6 + 2 * pi * n <= t <= 7*pi/6 + 2*pi*n, при любом целом n.
Exemplul 2. Rezolva cos inegalitate (t) <1/2.
Desenați un cerc unitate. Deoarece prin definiție, cos (t) este coordonata X, pe nota la punctul Ox grfike x = 1/2.
Atragem prin acest punct o linie paralelă cu axa y. Intersecția liniei drepte cu programul de cercul unitate marchează punctul PT1 și Pt2. Am conecta cele două segmente de origine la punctul PT1 și Pt2.
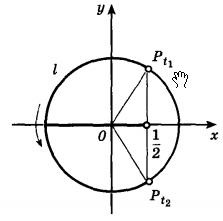
Deciziile sunt toate punctele cercului unitate, care aparțin unui arc l. Găsiți punctul de t1 și t2.
t1 = arccos (1/2) = pi / 3.
t2 = 2 * pi - arccos (1/2) = 2 * pi-pi / 3 = 5 * pi / 6.
Inegalitatea primite pentru t: pi / 3 Deoarece cosinusul - această funcție este periodică, atunci soluția va fi repetată la fiecare 2 * pi. Această condiție se adaugă la inegalitatea rezultată pentru T și scrie răspunsul. Răspuns: pi / 3 + 2 * pi * n Exemplul 3. Solve tg (t) inegalitate <= 1. tangenta perioadei este egal cu pi. Noi găsim soluții care aparțin intervalului (pi / 2; pi / 2), semicercul din dreapta. În continuare, folosind periodicitatea tangenta, vom scrie toate soluțiile inegalității. Desenați un cerc unitate și marcați pe ea linia de tangentele. Dacă t va fi o soluție a inegalității, ordonata punctului T = tg (t) trebuie să fie mai mic sau egal cu 1. Setul de puncte va constitui o grindă AT. Setul de puncte Pt, care va corespunde cu punctele grinzii - arc l. Mai mult, punctul P (pi / 2) nu aparține acestui arc. Condițiile în care Pt unele punct va aparține unui arc l. t1 = arctg (1) = pi / 4. Obținem inegalitate pi / 2 Având în vedere perioada de răspuns a scrie tan. Raspuns: pi / 2 + pi * n
Am nevoie de ajutor la școală?
articole similare