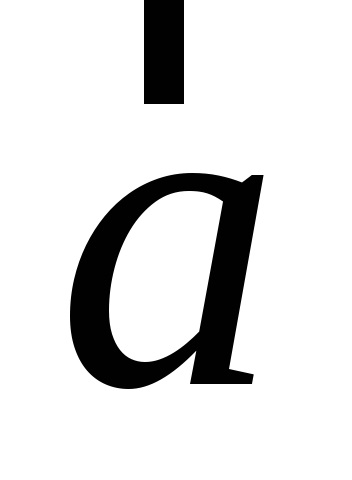Proiecția vectorului pe axa

Axa se numește linia direcționată.

Determinare. orth axa

Se numește versorul

, a cărei direcție coincide cu direcția axei.

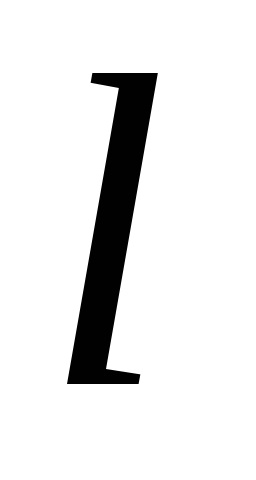
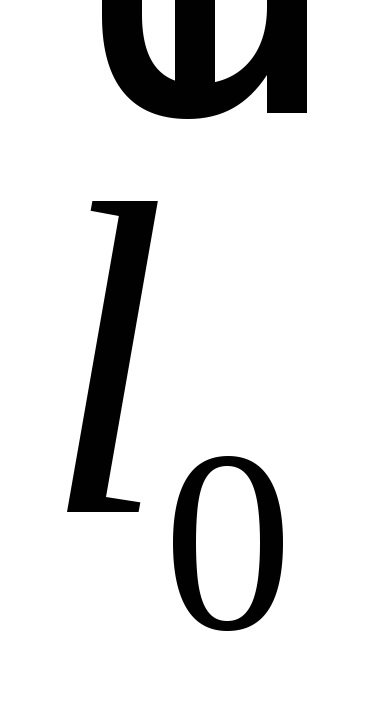
Determinare. Proiecția ortogonală M pe axa

numita bază M1 perpendicular de la M la

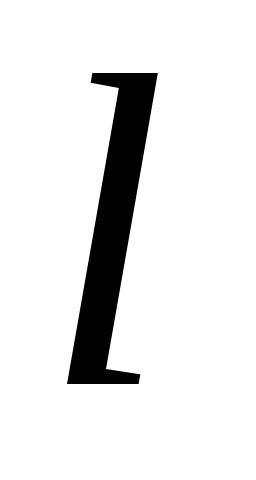
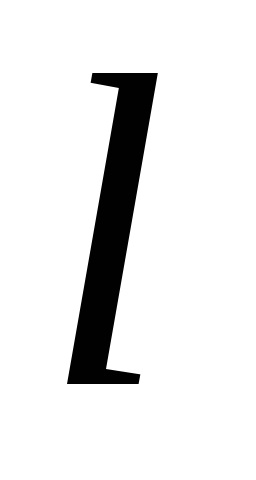
Determinare. vector Ortogonalnoyproektsiey

osie

nazyvaetsyadlina segmentul A1 B1 al acestei axe, încheiat între proiecțiile ortogonale de început și de sfârșit, luat de la semnul „+“ în cazul în care vectorul de direcție

Ea coincide cu direcția axei, și cu semnul „-“ în cazul în care direcțiile sunt opuse (figura 8.).

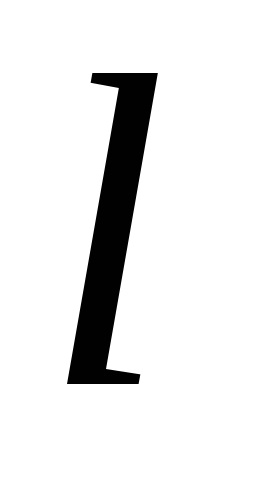
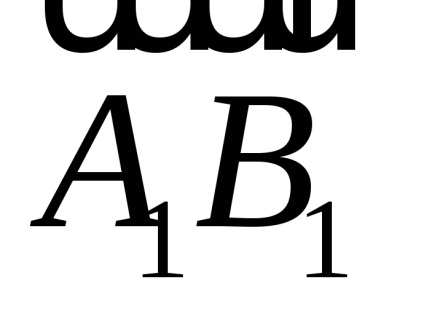
Determinare. Unghiul dintre vectorul și axa este unghiul la care doriți să se rotească în direcția pozitivă a axei sale în coincidență cu direcția de direcția vectorului (considerat pozitiv invers acelor de ceasornic rotație).

Evident, proiecția vectorului pe axa poate fi găsită prin formula

Se poate demonstra că proiecția este o combinație liniară a vectorilor de aceeași combinație liniară a proiecțiilor lor:

În special, proiecția sumei vectorului este egală cu suma proiecțiilor lor:

Să considerăm un sistem de coordonate cartezian rectangular HOY. denota

- vectorul unitar al axei x,

- Ort osiOY. Alegeți un punct

, și lăsați

- proiecții ale acesteia asupra OX iOY, adică coordonatele acestui punct (figura 9.).

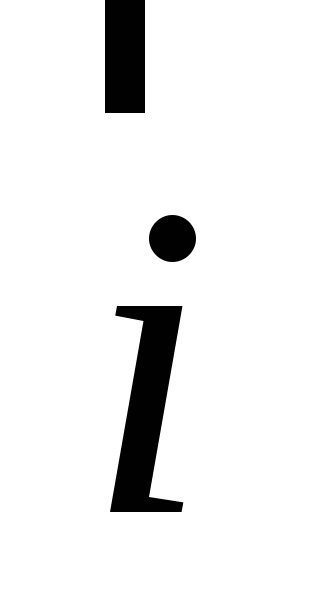
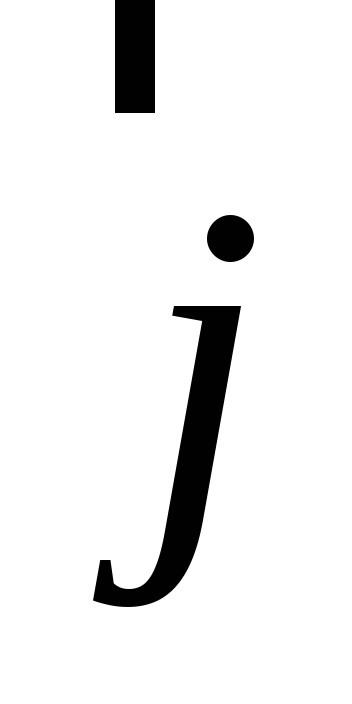
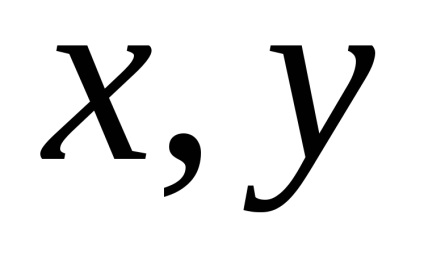
Astfel, dacă un anumit sistem cartezian rectangular (pdsk) coordonează, cu toate vectorul spațial

puteți lega cele trei numere

(sau două numere

, dacă vectorul este plat), care sunt coeficienții de dilatare ale vectorului pe vectori bază axelor de coordonate, precum sunt proiecțiile vectorului pe axele de coordonate.

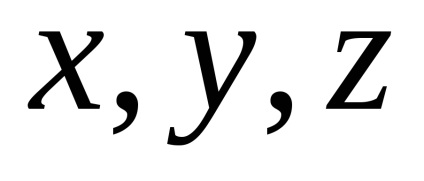
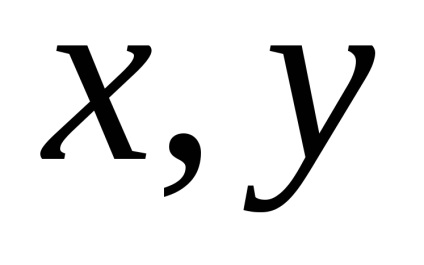
Determinare. coordonatele vectoriale

în lyuboypdsk numite coeficienți în extinderea vectorului unitar vectorii axelor de coordonate.

Astfel, putem da o altă definiție a vectorului.

Determinare. Un vector este ordonată triplu de numere (o pereche ordonată, în cazul în care vectorul este plat).

EXEMPLU. În cazul în care, atunci

= (2,3,4), și invers, dacă

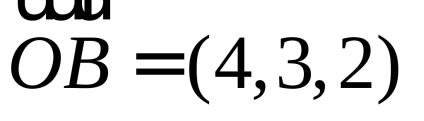
Deoarece, pe de o parte, vectorul - obiectul având o lungime și direcție, iar pe de altă parte, - un triplu ordonat de numere, cunoscând lungimea și direcția, se poate determina poziția și vice-versa. Vectorul de direcție într-un sistem de coordonate predeterminat, caracterizat prin cosinusului sale direcție (Figura 11):

articole similare

Pagina anterioară

Pagina următoare